
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Сила тиску рідини на дно посудини не залежить від форми посудини
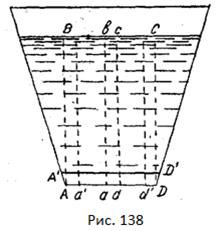 Розглянемо, чому дорівнює тиск рідини на дно посудини, зображеної на рис. 138. Виділимо в тонкий шар рідини A'ADD', що безпосередньо прилягає до дна посудини, і в ньому маленькі площинки Aa', ad, d'D (частини площинки дна). Виділений шар обмежений згори шарами рідини, що лежать над ним, з боків — стінками посудини і знизу — дном посудини. Отже, наш шар лежить у замкненому просторі. Сила тиску на площинку, що обмежує цей шар, очевидно, дорівнюватиме вазі вертикального стовпа (ABCD). За законом Паскаля ця сила тиску передаватиметься у замкненому шарі A'ADD' у всі сторони рівномірно. Отже, тиск на кожну площинку дна посудини, наприклад на площинку Aa', d'D, буде однаковий. Сила тиску на дно посудини дорівнює сумі всіх сил тисків на окремі площинки і дорівнює вазі вертикального стовпа ABCD, основою якого є дно посудини і висотою — висота стовпа від дна до рівня рідини.
Розглянемо, чому дорівнює тиск рідини на дно посудини, зображеної на рис. 138. Виділимо в тонкий шар рідини A'ADD', що безпосередньо прилягає до дна посудини, і в ньому маленькі площинки Aa', ad, d'D (частини площинки дна). Виділений шар обмежений згори шарами рідини, що лежать над ним, з боків — стінками посудини і знизу — дном посудини. Отже, наш шар лежить у замкненому просторі. Сила тиску на площинку, що обмежує цей шар, очевидно, дорівнюватиме вазі вертикального стовпа (ABCD). За законом Паскаля ця сила тиску передаватиметься у замкненому шарі A'ADD' у всі сторони рівномірно. Отже, тиск на кожну площинку дна посудини, наприклад на площинку Aa', d'D, буде однаковий. Сила тиску на дно посудини дорівнює сумі всіх сил тисків на окремі площинки і дорівнює вазі вертикального стовпа ABCD, основою якого є дно посудини і висотою — висота стовпа від дна до рівня рідини.
Добутий висновок, що безпосередньо виходить з закону Паскаля, можна перевірити на такому приладі (рис. 139). Прилад складається із чашечки А, дно якої підтримується важелем В, навантажуваним гирею. Під впливом сили тиску рідини дно чашечки відпадає, коли сила тиску на дно перевищить силу, що затримує дно біля країв чашечки. Вставляючи в чашечку різної форми посудини і наливаючи в них воду, можна виявити, що, не зважаючи на різну форму посудин, дно в них відпадає при однакових рівнях води. Це вказує на те, що тиск рідини на дно посудини не залежить від форми посудини.
Виведена формула для визначення сили тиску на дно в циліндричній посудині: 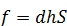 , справедлива і для посудини будь якої форми.
, справедлива і для посудини будь якої форми.
Силу тиску рідини на дно посудини не треба плутати з вагою цієї рідини. Якщо позначити вагу рідини буквою Р, силу тиску на дно буквою F, то для циліндричної посудини матимемо рівність F=P, для посудини конічної форми, звуженої угорі, очевидно, F > Р, і для посудини, розширеної вгорі, F<P.
Запитання та вправа.
1. Виходячи з закону Паскаля, довести, що тиск рідини на дно посудини не залежить від форми посудини.
2. Яке співвідношення між вагою рідини і її силою тиску на дно посудини: 1) у циліндричній посудині; 2) у конічній посудині, розширеній вгорі, і 3) у конічній посудині, розширеній внизу ?
3. Обчислити, з якою силою тисне спирт на дно посудини, якщо площа дна посудини 25 см2, а висота стовпа спирта 15 см.
4. Широка трубка у формі зрізаного конуса занурена у воду, нижній отвір її закритий пластинкою. Площа основи пластинки 30 см, а глибина занурення пластинки 10 см. Якої найменшої ваги гирю треба покласти на пластинку, щоб вона відірвалась ?
Закон сполучених посудин
У сполучених посудинах одна і та сама рідина при рівновазі стоїть на однаковім рівні.
Цей перевірений на досліді факт виходить безпосередньо з закону Паскаля. Нехай А і В (рис. 140) дві сполучених посудини, у яких рідини відокремлені одна від одної тонкою площиною S, яка легко може пересуватися. Коли рідина в посудині перебуває в рівновазі, площинка буде також у рівновазі. Розглянемо сили тиску, яких зазнає  наша площинка від рідини. Позначимо висоту стовпа рідини в посудині А буквою
наша площинка від рідини. Позначимо висоту стовпа рідини в посудині А буквою 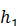 , а в посудині В буквою
, а в посудині В буквою 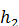 , питома вага рідини нехай буде d. Сила тиcку від посудини А на площинку дорівнює
, питома вага рідини нехай буде d. Сила тиcку від посудини А на площинку дорівнює 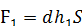 , а від посудини В сила
, а від посудини В сила 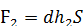 . Площинка буде в рівновазі, якщо
. Площинка буде в рівновазі, якщо  , або
, або 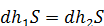 , звідки, скоротивши на dS, отримаємо
, звідки, скоротивши на dS, отримаємо 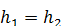 , що й треба було довести.
, що й треба було довести.
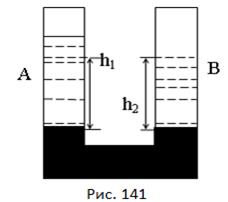 Наллємо в трубку, що сполучає посудини, ртуті, в посудини А і В (рис. 141) — різних рідин, наприклад, в одне коліно —води, а в друге — гасу так, щоб рівні ртуті в посудинах були однакові. При цих умовах тиски на поверхню ртуті в обох
Наллємо в трубку, що сполучає посудини, ртуті, в посудини А і В (рис. 141) — різних рідин, наприклад, в одне коліно —води, а в друге — гасу так, щоб рівні ртуті в посудинах були однакові. При цих умовах тиски на поверхню ртуті в обох
колінах будуть однакові. Позначимо питому вагу гасу буквою d1 висоту стовпа буквою h1, питому вагу води буквою d2 і висоту стовпа її буквою h2. Тоді, на підставі попереднього, 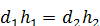 , звідки:
, звідки:
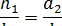
Висоти, стовпів різнорідних рідин у сполучених посудинах обернено пропорційні до питомої ваги рідин.
Закон сполучених посудин широко застосовується в техніці й житті. Наприклад, паровий казан має водомірне скло, за рівнем води в якому визначають висоти води в казані. На підставі цього ж таки закону роблять різні фонтани, артезіанські колодязі, постачають міській людності воду із спеціальних резервуарів, розміщених на високому місці, і т. д.
Застосування сполучених посудин можна бачити в шлюзах, які влаштовують для спокійного проходу суден на порожистих ріках.
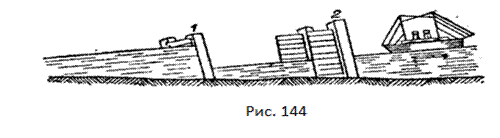 |
Наприклад, судноплавство на Дніпрі біля Дніпрогесу забезпечується розміщеним на лівому березі шлюзом. Шлюз складається з трьох камер; у кожній з них судно опускається або підіймається, наприклад, на 12 м. Розмір камер: довжина 120 м, ширина 18 м і мінімальна глибина 3,6 м. Спускаючи судно з верхів'їв, його підводять до воріт, і тут воно стоїть, поки в шлюзову камеру набереться вода (рис. 142) до рівня води перед ворітьми шлюзу. Коли рівні зрівняються, ворота відкривають 1 судно переходить у шлюзову камеру (рис. 143). Ворота 1 за судном закривають і з шлюзової камери спускають воду, аж поки її рівень зрівняється з рівнем води за ворітьми 2. Те саме роблять з третьою камерою. Коли рівень у третій камері зрівняється з рівнем води за ворітьми цієї камери, їх відкривають, і судно переходить через аванпорт у річку (рис. 144). Коли судно йде вгору, наповнюючи послідовно камери водою при закритих тепер задніх воротах, його підіймають до найвищого верхнього рівня води.
Запитання та вправи.
1. В чому полягає закон сполучених посудин для однорідної рідини, для різнорідної рідини ?
2.  Які, крім перелічених у тексті, є застосовування сполучених посудин ?
Які, крім перелічених у тексті, є застосовування сполучених посудин ?
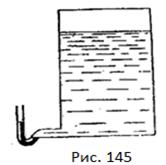
3. На рис. 145 показано водяний бак із ртутною пробкою. Якої висоти має бути стовп ртутної пробки, щоб ним можна було зрівноважити водяний стовп висотою на 136 см ?
4. У сполучені посудини налита ртуть. До якої висоти треба налити в одне коліно гасу, щоб ртуть в другому коліні піднялася на 2 см ?
5. Як можна визначити питому вагу рідини за допомогою сполучених посудин ?
Закон Архімеда
Рідина, що перебував в рівновазі, тисне не тільки на дно та стінки посудини, а й на всяке занурене в неї тіло. Розглянемо силу тиску рідини на прямокутну призму ABCD з основами, паралельними до поверхні рідини (рис. 146). Через те, що тиск усередині рідини поширюється у всі сторони, кожна частина поверхні нашої призми зазнаватиме певну силу тиску, яка залежить від величини її площ та глибини її занурення.
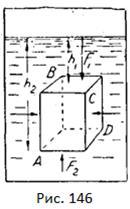 Сили тиску на бічні стінки призми ABCD рівні між собою і протилежно спрямовані, через це вони взаємно зрівноважуються; під впливом їх тіло тільки стискуватиметься. Залишається розглянути силу тиску на горизонтальні грані призми BC і AD. На верхню основу BC рідина тисне з силою F1 = Sdhl; де d — питома вага рідини, S—площа основи призми і h1 — висота стовпа від основи BC до рівня рідини. На нижню основу AD рідина тисне з силою F2=Sdh2, де h2— віддаль від AD до рівня рідини.
Сили тиску на бічні стінки призми ABCD рівні між собою і протилежно спрямовані, через це вони взаємно зрівноважуються; під впливом їх тіло тільки стискуватиметься. Залишається розглянути силу тиску на горизонтальні грані призми BC і AD. На верхню основу BC рідина тисне з силою F1 = Sdhl; де d — питома вага рідини, S—площа основи призми і h1 — висота стовпа від основи BC до рівня рідини. На нижню основу AD рідина тисне з силою F2=Sdh2, де h2— віддаль від AD до рівня рідини.
Отже, на тіло діють дві сили: одна F1, напрямлена згори вниз, і друга F2 — знизу вгору. Рівнодійна цих двох сил дорівнює їх різниці: F2 — F1 = Sdh2 — Sdh1 = Sd (h2 — h1) і напрямлена знизу вгору. Дією цієї сили тіло виштовхуватиметься із рідини вгору. Будемо називати цю силу підіймальною силою. Через те, що h2 — h1 висота призми, S(h2 — h1) - об'єм призми і d — питома вага рідини, права частина рівності є не що інше, як вага рідини, витисненої зануреним тілом.
Підіймальна сила, що діє на занурене в рідину тіло, дорівнює вазі рідини, витисненої тілом.
Цей закон відкрив Архімед. Називається він законом Архімеда.
Підіймальна сила, що діє на тіло, напрямлена протилежно до ваги цього тіла; тому, якщо тіло, занурене в рідину, зважити, то вага цього тіла буде менша від дійсної ваги на величину підіймальної сили; тут маємо позірну „втрату" ваги.
У тому, що підіймальна сила існує, можна пересвідчитися на найрізноманітніших дослідах. Наприклад, якщо в скляну посудину з рівним дном (рис. 147) впустити плоский і рівний кусок скла, до середини якого прикріплена ручка, і, придержуючи кусок, налити в  посудину ртуті, то скло залишається на дні. Ртуть, не протікаючи в простір між дном посудини і куском скла, тисне на нього згори вниз. Але, якщо лише злегка нахилити скло, ртуть відразу ж пройде під нього, виникне підіймальна сила, яка виштовхне скло на поверхню ртуті.
посудину ртуті, то скло залишається на дні. Ртуть, не протікаючи в простір між дном посудини і куском скла, тисне на нього згори вниз. Але, якщо лише злегка нахилити скло, ртуть відразу ж пройде під нього, виникне підіймальна сила, яка виштовхне скло на поверхню ртуті.
Якщо почепити на тонкій гумовій трубочці кусок цеглини, то трубочка дуже розтягнеться. Якщо цеглину опускати в воду, довжина гумової трубки дуже скорочується. Підіймальна сила води, діючи проти ваги цеглини, зменшує розтяг трубочки.
Через ту ж таки підіймальну силу ми без особливих зусиль пересуваємо під водою великі вантажі, які на поверхні води пересунути не могли.
Запитання та вправи.
1. Чому дорівнює величина підіймальної сили, що діє на тіло, об'єм якого 2 дм3, у воді, у спирті, у ртуті?
2. Чи змінюватиметься підіймальна сила при збільшенні глибини занурення тіла ? Вважаємо, що густина рідини однакова на будьякій глибині.
3. Чим пояснити, що, ходячи по дну річки, всипаному гострим камінням, ми не відчуваємо такого болю, який відчуваємо, ходячи по такому самому камінню на березі ?
Последнее изменение этой страницы: 2016-07-23
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...