
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Методика получения модели механических колебательной системы сосредоточенными параметрами на основе уравнений Лагранжа 2-ого рода
Во многих случаях при моделировании механических систем приемлемы предположения о том, что масса системы сосредоточена лишь в конечном числе точек, соединенных между собой элементами типа пружин (элементы, накапливающие потенциальную энергию) и типа "демпфер" (элемент, рассеивающий энергию), в этом случае математическая модель, описывающая повеление рассматриваемой системы представляет собой систему обыкновенных дифференциальных уравнений (ОДУ). Рассмотрим следующий пример.

По гладкой плоскости без трения под действием внешней силы, изменяющейся во
времени по закону P(t), движутся два груза (рис.1).
 |
Для построения математической модели следует воспользоваться уравнениями Лагранжа 2-го рода, которые приводят к системе двух обыкновенных дифференциальных уравнений второго порядка [1].
 Здесь x1(t) и x2(t) - смещения относительно положения равновесия соответственно 1-й и 2-й массы;
Здесь x1(t) и x2(t) - смещения относительно положения равновесия соответственно 1-й и 2-й массы;
- скорости смешений относительно положения равновесия соответственно 1-й и 2-й массы, где t - время;
Т - кинетическая энергия системы; П - потенциальная энергия системы.
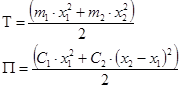 | 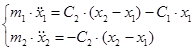 | ||
В качестве 1 - й и 2- й степеней свободы примем x1 и x2.
Тогда уравнения примут вид:
Выполнение этого этапа базируется на использовании знаний курса теоретической механики. Подробности можно найти в книгах [1,2]. Результатом выполнения этого этапа являются уравнения. движения механической системы. Их подробный вывод следует привести в отчете.
Системы с рассредоточенными параметрами- в этой ситуации неизвестные величины(напр. Перемещение точек) являются уже функ-ми нескольких переменных. Поведение таких систем чаще всего описывается ДУЧП. Виды: 1)Метод граничных элементов 2)Метод конечных элементов 3) Метод сеток.
Интерполирование, алгебраическое интерполирование, классический подход
Интерполирование – это вид приближения, если приближенную функцию обозначить 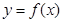 , то для таблицы из n точек
, то для таблицы из n точек  ,
, 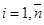 необходимо потребовать выполнения условия:
необходимо потребовать выполнения условия:
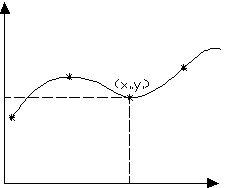

Понятно, что в такой общей постановке решением задачи может оказаться бесконечное решение функций, поэтому, чтобы сделать задачу определенной, необходимо сузить класс подбираемых функций. Как было рассмотрено выше, при наличии определенной информации следует подбирать приближенную функцию так, чтобы она согласовывалась с приближаемыми данными.
Если же такой информации нет, то одним из способов выбора является выбор полинома в качестве приближаемой функции. В этом случае интерполяцию называют алгебраической.
Будем искать интерполянт в виде полинома степени не выше(n-1).
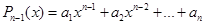 (1)
(1)
Тогда условие (1) примет вид:
 (2)
(2)
Понятно, что вид интерполирующего полинома полностью определяется набором коэффициента.
Рассмотрим следующее утверждение:
Пусть в n попарно-различных точках 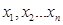 заданы числа
заданы числа  , тогда существует единственный полином
, тогда существует единственный полином 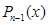 степени не выше (n-1), удовлетворяющий условию (*).
степени не выше (n-1), удовлетворяющий условию (*).
Доказательство:
Запишем это условие в каждой точке
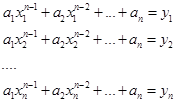
Здесь 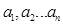 - неизвестные, а правые части известны:
- неизвестные, а правые части известны:
 (4)
(4)
Эта матрица специального вида - матрица Вандерманда. Для нее легко показать, что определитель этой матрицы 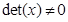 отличен от нуля, но если это так, то система (4) имеет единственное решение.
отличен от нуля, но если это так, то система (4) имеет единственное решение.
Следствием этого утверждения является то, что вид интерполирующего полинома не зависит от способа его построения. А сам ход рассмотренных рассуждений дает один из способов построения такого полинома.
Рассмотренный способ называется классическим, т.к. в силу единственности интерполяционного полинома, каким бы способом его не строили, результат будет один и тот же.
Пример получения математической модели для двух массовой колебательной системы
 q1 – линейное перемещение верхней массы
q1 – линейное перемещение верхней массы
q2 – нижней
q1, q2 – абсолютное перемещение (от земли)
 -уровень земли
-уровень земли
Выразим удлинение упругих элементов конструкции  и
и  Найдём:
Найдём:

Последнее изменение этой страницы: 2016-08-11
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...