
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Метод типа Рунге-Кутта для решения задачи Коши
y(x+h) = y(x) + 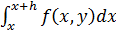

Выполним замену переменной 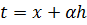
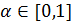
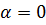 t=x
t=x
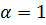 t=x+h
t=x+h 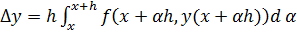
Введем три набора параметров 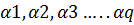
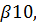 …..
…..
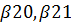 …..
…..
………………
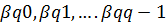
A0,A1,…..Aq
При помощи  и
и 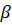 наборов будем последовательно вычислять величины.
наборов будем последовательно вычислять величины.
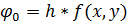
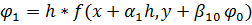

………..
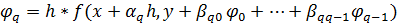
Эти величины могут быть вычислены последовательно. Теперь при помощи параметров группы А составим линейную компбинацию.
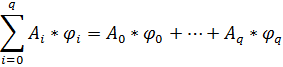
Будем приближать величину 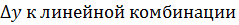 т.е.
т.е.
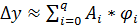 Погрешность этого приближения обозначим
Погрешность этого приближения обозначим 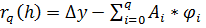 . Разложим по формуле Тейлора
. Разложим по формуле Тейлора
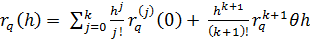
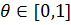 (1) Основная идея этого подхода в том, чтобы подобрать такие наборы (
(1) Основная идея этого подхода в том, чтобы подобрать такие наборы (  ), которые обеспечили бы как можно лучшее приближение
), которые обеспечили бы как можно лучшее приближение  к составленной линейной комбинации. Это значит, что при произвольной функции f в выражении 1 как можно большее количество слагаемых в формуле Тейлора оказались =0 т.е. чтобы
к составленной линейной комбинации. Это значит, что при произвольной функции f в выражении 1 как можно большее количество слагаемых в формуле Тейлора оказались =0 т.е. чтобы  для как можно большего k.
для как можно большего k.
Методы 1-го порядка точности.
Пусть q=0 тогда А0 тогда  после вычисления
после вычисления 
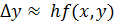
y(x+h) 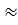 y(x)+hf(x,y) Мы получим формулу метода Эйлера, это значит что частный случай метода Рунге-Кутта.
y(x)+hf(x,y) Мы получим формулу метода Эйлера, это значит что частный случай метода Рунге-Кутта.
Использование встроенных функций для линейной аппроксимации по методу наименьших квадратов
Vx и Vy – заранее сформированные массивы абсцисс и ординат .
m:=slope(vx,vy)
b:=interapt(vx,vy)
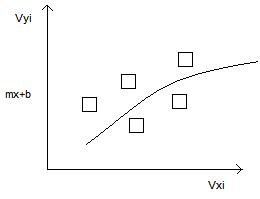 x- Массив точек в который мы хотим вычленить mx+b
x- Массив точек в который мы хотим вычленить mx+b
Связь модифицированных методов Эйлера и методов Рунге-Кута второго порядка для решения задачи Коши
Методы второго порядка.q=1,∆y≈Ao*ϕо+Aо*ϕ1,в этой ситуации у нас есть параметры α1,β10,Ао,А1. Можно показать, что эти четыре величины оказываются связанными между собой следующей системой нелинейных уравнений :
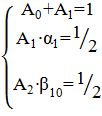
как видно количество уравнений меньше числа неизвестных ,это позволяет положить один из параметров равным какому-то значению, а остальные три определить через него
α1= β10=1/2А1,
Aо=1- A1,
А1=1/2,
Ао=1/2,
α1= β10=1,
∆y≈Ao*ϕо+A1*ϕ1,
ϕо=h*f(x,y),
ϕ1=h*f(x+h,y+ ϕо),
Пусть A1=1,A0=0, α1= β10=1/2, тогда
∆y≈ ϕ1,
ϕо=h*f(x,y),
ϕ1=h*f(x+h,y+ ϕо) это другая модификация метода Эйлера.
Могут быть получены и др. формулы метода второго порядка, и как видно модификации метода Эйлера-частные случаи метода Рунге-Кутта. Приведем систему уравнений для методов 3-го порядка.
q=2
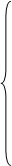 A1+A2+A0=1,
A1+A2+A0=1,
A1* α1+A2* α2=1,
A1* α1+A2* α2=1/3,
A2* α1* β21=1/6,
β20+ β21= α2,
β10= α1,
∆y≈1/6(ϕо+ 4* ϕ1+ ϕ2),где ϕо=h*f(x,y),
ϕ1=h*f(x+h/2,y+ ϕо/2),
ϕ2=h*f(x+h,y- ϕо + 2ϕ1),
∆y≈  ( ϕ0+3 ϕ2),
( ϕ0+3 ϕ2),
ϕо=h*f(x,y),
ϕ1=h*f(x+h/3,y+ ϕо/3),
ϕ2=h*f(x+2/3*h,y- ϕо + 2/3*ϕ1)
Понятие о сплайнах
Функция Sn,ν (x) – сплайн степени n дефекта ν, где n и ν - целые числа, если
1) на каждом из отрезков (xi, xi+1) из (a,b) функция Sn,ν (x) является полиномом степени n;
2) если Sn,ν (x) на всем интервале (a,b) имеет непрерывные производные до порядка
n- ν включительно.
Кусочные полиномы, образующие сплайн, называются звеньями, а условия непрерывности в узлах____
Рассмотрим сплайн 1-ой степени S1(x). Он представляет собой непрерывную кусочно-линейную функцию. На каждом из отрезков (xi, xi+1) он является полиномом 1-ой степени:
S1 (x) = A0+A1∙x
ν=1, т.е. непрерывной производной он не имеет.
Уравнение сплайна:
S1(x) = 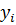 +
+ 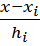 (
(  ), xi
), xi  i+1
i+1
hi =xi+1 – xi - шаг
Для построения этого сплайна требуется только таблица (xi ,yi). Вычисление этого сплайна можно выполнять по следующему алгоритму:
1) определение tg угла наклона:
tgαi =  =
= 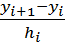
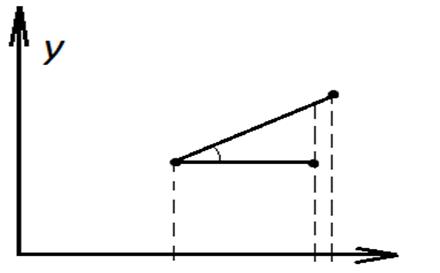
и вычисляется S1 (x)= 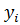 +Ui ∙ (x – xi ).
+Ui ∙ (x – xi ).
 (xi+1,yi+1)
(xi+1,yi+1)

 Ui(x-xi)
Ui(x-xi)
 (xi,yi) α
(xi,yi) α
S1(x)
yi
xi x xi+1
Сплайн 1-ой степени относится к семейству локальных сплайнов, т.к. для его построения необходима информация только об ограничивающих данный участок узлах.
20.1 Метод Рунге-Кута 4-ого порядка для решения задачи Коши формулы метода 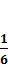 и их реализация в среде MathCad
и их реализация в среде MathCad
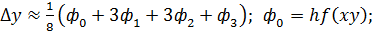
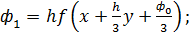
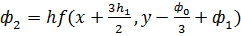 ;
; 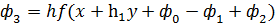
___________________________________________________________________________
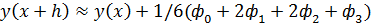
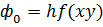
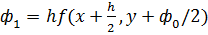
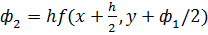
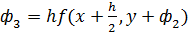
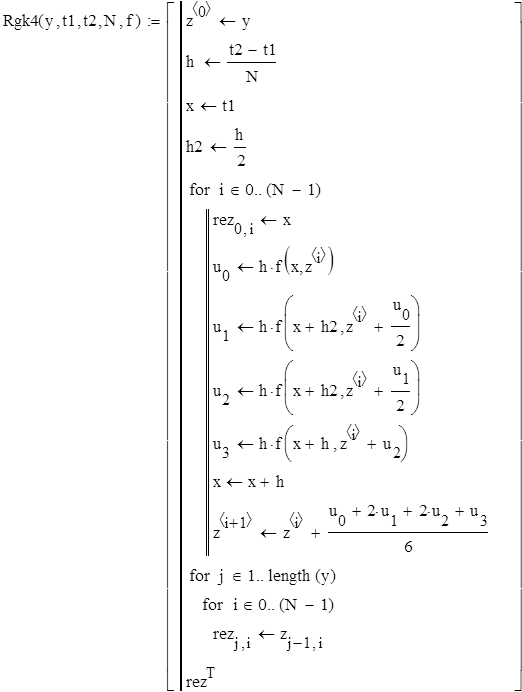
|
20.2 Определение сплайна. Дефект сплайна, пример линейного сплйна
Функция Sn,ν (x) – сплайн степени n дефекта ν, где n и ν - целые числа, если
3) на каждом из отрезков (xi, xi+1) из (a,b) функция Sn,ν (x) является полиномом степени n;
4) если Sn,ν (x) на всем интервале (a,b) имеет непрерывные производные до порядка
n- ν включительно.
Кусочные полиномы, образующие сплайн, называются звеньями, а условия непрерывности в узлах____
Рассмотрим сплайн 1-ой степени S1(x). Он представляет собой непрерывную кусочно-линейную функцию. На каждом из отрезков (xi, xi+1) он является полиномом 1-ой степени:
S1 (x) = A0+A1∙x
ν=1, т.е. непрерывной производной он не имеет.
Уравнение сплайна:
S1(x) = 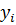 +
+ 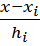 (
(  ), xi
), xi  i+1
i+1
hi =xi+1 – xi - шаг
Для построения этого сплайна требуется только таблица (xi ,yi). Вычисление этого сплайна можно выполнять по следующему алгоритму:
2) определение tg угла наклона:
tgαi =  =
= 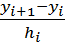
и вычисляется S1 (x)= 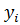 +Ui ∙ (x – xi ).
+Ui ∙ (x – xi ).

 (xi+1,yi+1)
(xi+1,yi+1)

 Ui(x-xi)
Ui(x-xi)
 (xi,yi) α
(xi,yi) α
S1(x)
yi
xi x xi+1
Сплайн 1-ой степени относится к семейству локальных сплайнов, т.к. для его построения необходима информация только об ограничивающих данный участок узлах.
Последнее изменение этой страницы: 2016-08-11
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...