
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Оценка погрешности решения ОДУ. Способ Рунге для оценки такой погрешности.
Основная цель приближённых вычислений заключается в нахождении результата с заданной степенью точности. В частности для оценки точности решения ДУ можно использовать такие способы:
1. Проверка выполнения условия задачи (например данное численное решение можно подставить в само ДУ и сравнить расхождение с его правой частью)
2. Двойной пересчет по возможности другим методом
3. Применение упрощённой расчетной схемы и качественный анализ задачи.
Локальная погрешность тем меньше, чем меньше шаг, в то же время при большом количестве шагов суммарная погрешность может возрастать. Если же шаг увеличить хотя время решения задачи сократится полученная точность может не удовлетворять исследователя. Для приближенной оценки точности решения можно использовать способ Рунге.
Способ Рунге для оценки такой погрешности.
Предполагает, что на зад. интервале решение выполняется с постоянным по величине шагом, а затем решение выполняется с удвоенным по величине шагом H=2h. Пусть при этом используется метод m-го порядка точности. Тогда на отдельном шаге h величина локальной погрешности составит:  .
.
Предполагаем, что c шагом h выполняется 2n шагов, тогда Н→n.
Предположение на котором основан метод Рунге заключается в том, что на отдельном шаге погрешность равна: 

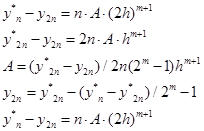
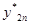 - приближенное решение в конечной точке tk после 2n шагов величины h.
- приближенное решение в конечной точке tk после 2n шагов величины h.
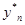 - приближенное решение в точке tk после n шагов величиной H=2h.
- приближенное решение в точке tk после n шагов величиной H=2h.
Y2n – неизвестное решение.
Считая на каждом шаге погрешность одинаковой, можно записать:
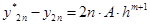
При вычислении с удвоенным шагом:


Система двух уравнений с двумя неизвестными A и Y2n. Решая, получим:
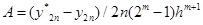

Уклонение точного решения от приближенного:
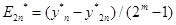
В частности для более распространенного метода Рунге-Кутта 4-го порядка (m=4):
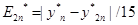
Ещё раз заметим, что в основе этой оценки лежит предположение, что на отдельном шаге погрешность равна 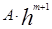
21.2 Кубический сплайн дефекта 2 (или сплайн Эрмита).
Сплайн на интервале  является кубическим полиномом
является кубическим полиномом
 (2)
(2)
и на всем интервале 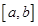 имеет непрерывную производную.
имеет непрерывную производную.
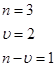
Для определения коэффициентов в формуле (2) используем условие прохождения сплайна через узлы, то есть
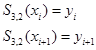 (3)
(3)
Добавим к ним условия непрерывности в узлах:
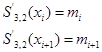 (4)
(4)
где 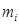 - тангенс угла наклона сплайна.
- тангенс угла наклона сплайна.
Условия (3) и (4) образуют систему линейных дифференциальных уравнений относительно коэффициентов 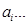 . Если решить эту систему и подставить значения коэффициентов в формулу (2), то получим следующий вид:
. Если решить эту систему и подставить значения коэффициентов в формулу (2), то получим следующий вид:
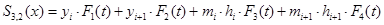 (4)
(4)
где  - длина интервала, а
- длина интервала, а  - полиномы Эрмита.
- полиномы Эрмита.

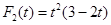
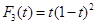
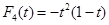
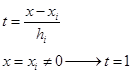
Как видно из формулы (5) необходимо знать кроме значений 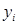 и наклон в узле. В практических задачах наклоны обычно неизвестны. В этом случае поступают так: эти наклоны предварительно вычисляют по формулам приближенного дифференцирования.
и наклон в узле. В практических задачах наклоны обычно неизвестны. В этом случае поступают так: эти наклоны предварительно вычисляют по формулам приближенного дифференцирования.
Без вывода приведем формулы для вычисления этих наклонов. Во внутренних точках интервала формулы имеют вид:
 (6)
(6)
где 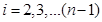
Для крайних точек формулы имеют вид:
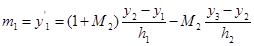 (7)
(7)
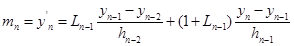 (8)
(8)
где 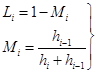 (9)
(9)
Алгоритм построения данного сплайна:
Проверить на какой из отрезков (xi, xi+1) попадает значение аргумента х. Если значение аргумента совпало с одной с одной из двух границ подинтервала, то значение сплайна равно табличному значению интерполируемой функции, в противном случае нужно вычислить значение безразмерной переменной t, вычислить значение эрмитовых функций. Если подинтервал является внутренним, то воспользоваться формулами 6 для приближённых вычислений наклонов на его концах. Если внешний, то для одного конца нужно исп. формулу 6, а для другого одну из формул 7, 8. И теперь по формуле 4 посчитать значение Эрмитова сплайна.
Метод стрельбы
Пусть имеется ДУ 2-го порядка 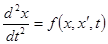 (1)
(1)
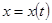 - неизвестная функция, являющаяся решением ДУ(1), которая должна удовлетворять след условиям в начальный и конечный момент наблюдения t0 и tк.
- неизвестная функция, являющаяся решением ДУ(1), которая должна удовлетворять след условиям в начальный и конечный момент наблюдения t0 и tк.
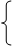
 (2)
(2)
 заданные числа
заданные числа
Примером может служить выбор траектории полёта снаряда, выпущенного из орудия которое находится на заданной высоте. Ствол орудия наклонен так, что в конечный момент времени снаряд должен оказаться на другой заданной высоте.
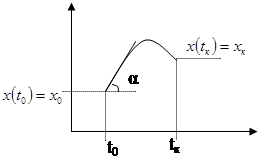 |
Моменты t0 и tк являются границами интервала изменения независимой переменной, на котором нужно получить решение. Поэтому условие 2 задающее нужные значения решения для этих границ называется граничным условием. Соответственно задача 1 и 2 это граничная задача для ДУ.
Нужно заменить граничную задачу начальной.
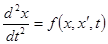 (1)
(1)
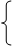
 (3)
(3)
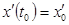
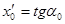 |
Т.о. нужно подобрать угол наклона орудия (пристреляться) так, чтобы при tк высота на которой окажется снаряд была заданной. В этом и заключается идея метода пристрелки.
Кубические сплайны дефекта 1
Это сплайны, которые произошли от гибкой линейки чертёжника при этом в узлах непрерывна должна быть 1-ая и 2-ая производная.
 уравнение изогнутой оси балки, когда заданы изгибные моменты в каждой точке. По аналогии 2-ые производные будем называть моментами.
уравнение изогнутой оси балки, когда заданы изгибные моменты в каждой точке. По аналогии 2-ые производные будем называть моментами.

Пусть в n попарно различных точках отрезка [a,b] a<x1<x2<x3….xn=b
y1=f(x1)…. Yn=f(xn)
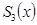 непрерывен на [a,b] вместе с 1-ой и 2-ой производной, совпадает с кубическим полиномом на каждом из отрезков и удовлетворяет условиям
непрерывен на [a,b] вместе с 1-ой и 2-ой производной, совпадает с кубическим полиномом на каждом из отрезков и удовлетворяет условиям  i=1..n
i=1..n
Поскольку 2ая производная по условию в каждом узле непрерывна, то введя обозначения  i=1,2…n и предположив, что
i=1,2…n и предположив, что 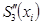 меняется линейно на интервале
меняется линейно на интервале 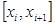 можно записать
можно записать  (1)
(1)
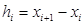
Проинтегрируем дважды (1). Интегрирование будем выполнять со скобкой. Тогда после 1-го интегрирования получим  (2)
(2)
А после второго интегрирования получим
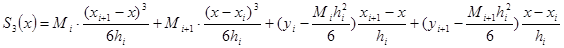 (3)
(3)
Это выражение мы получили для отрезка 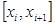 , аналогичное выражение мы можем получить для предыдущего отрезка
, аналогичное выражение мы можем получить для предыдущего отрезка
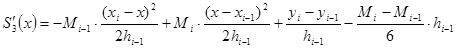 (4)
(4)
Используя условие непрерывности 1-ой производной для узла xi
Для этого приравняем (2) при x=xi к выражению (4) при x=xi . В результате получим
 (5)
(5)

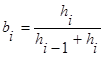
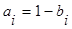 |
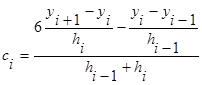 (6)
(6)
 (7) i=2,3…n-1
(7) i=2,3…n-1
Т.е. мы получили n-2 линейных алгебраических уравнения относительно Mi
Для замыкания этой системы нужно задать 2 дополнительных уравнения. Эти уравнения можно получить используя условие на концах интервала [a,b] (краевые условия)
1.Периодический сплайн T=b-a.
При этом предполагается, что интерполируемая функция периодическая с T=b-a и поэтому сам сплайн тоже должен быть периодическим с таким же периодом. Запишем условия периодичности:

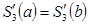

Тогда можно потребовать, чтобы уравнение (7) было справедливо и для i=n, а условие периодичности примет вид
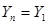
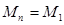
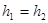
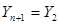
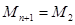
Тогда уравнение (7) примет вид
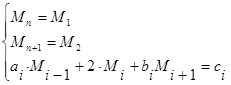 (8)
(8)
2.Непериодический сплайн с заданными наклонами в т a и b
 заданное число
заданное число
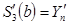 заданное число
заданное число
Запишем уравнение (2) при i=1 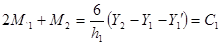
Если записать уравнение (3) при i=n 
Тогда замыкающая система примет вид
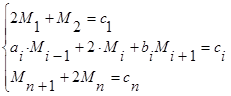 (9)
(9)
Решив системы 8 и 9 можно найти неизвестные M1…..Mn и можем построить сплайн в соответствии с формулой (3)
В некоторых случаях более удобно записывать сплайн в виде набора коэффициентов кубических полиномов вида
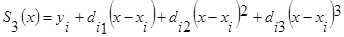 , где
, где 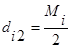
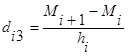
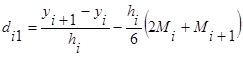 i=1,2..n-1
i=1,2..n-1
Последнее изменение этой страницы: 2016-08-11
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...