
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
ОТОПИТЕЛЬКО-ВАРОЧНАЯ ПЕЧЬ КОНСТРУКЦИИ В. А. ПОТАПОВА
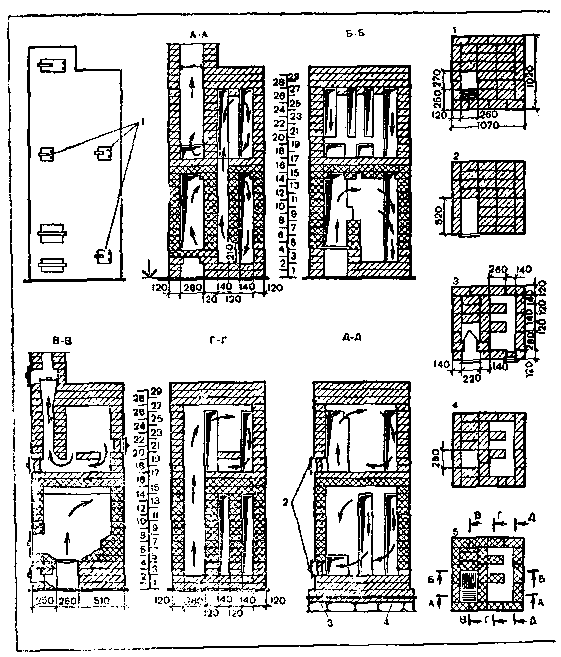
Размеры печи, мм; длина — 1160, ширина — 640, высота — 1890 (рис. 201). Теплоотдача при одной топке в сутки — 2400 ккал/ч, при двух — 3900 ккал/ч.
Печь с плитой В. А. Потапова работает на в-сех видах твердого топлива. Имеет летний и зимний ходы, варочную камеру с вентиляционным каналом, духовой шкаф, водогрейную коробку, две дымовые задвижки. При топке в летнее время открывают нижнюю задвижку, в зимнее — верхнюю (нижнюю при этом закрывают) .
Варочную камеру закрывают дверцей из двух половинок. При увеличении высоты печи сверх указанной верхнюю часть ее приходится перекрывать тремя рядами кладки плашмя. При топке каменным углем или антрацитом топку следует выполнять из огнеупорного кирпича, спустив при этом колосниковую решетку ниже на один ряд кладки.
Для кладки печи требуются: глина, песок, кирпич красный — 580 шт., топочная дверца размером 200X210 мм, дверца варочной камеры — 620X420 мм, две дымовые задвижки — 270X140 мм, духовой шкаф — 450X570X350 мм, водогрейная коробка — 120X580X205 мм, проволока, гвозди, полосовая сталь.
Кладка подробно рассмотрена в порядовках.

Pис. 202. Отопительная печь конструкции Н. С. Подгородникова (типа двухъярусный колпак):
1,2 — чистка; 3 — гидроизоляция; 4 — фундамент
ОТОПИТЕЛЬНО-ВАРОЧНАЯ ПЕЧЬ
КОНСТРУКЦИИ И. С. ПОДГОРОДНИКОВА
(ТИПА «ДВУХЪЯРУСНЫЙ КОЛПАК»)
Размеры печи, мм: длина — 1070, ширина — 1020, высота — 2100. Состоит из двух колпаков, поставленных друг на друга (рис. 202). Горячие газы скачала нагревают нижний, а затем верхний колпак. Нижний колпак поглощает 80% тепла, верхний — 20%. При двух топках теплоотдача составляет 4000 ккал/ч. Конструкция печи такова, что разница температуры у пола и потолка не превышает 2 — 4 °С. Печь лучше всего класть в стальных футлярах (коробах) с установкой герметически закрываемых дверец.
Для кладки печи требуется: красный кирпич — 430 шт., огнеупорный — 270 шт., глина, песок, колосниковая решетка — 300X250 мм, топочная дверца — 250X200 мм, поддувальная дверца (250X140 мм), шесть дверец для чистки (130X140 мм), вьюшечная дверца (320X140 мм) и вьюшка с отверстием 220мм,
ОТОПИТЕЛЬНАЯ ПРЯМОУГОЛЬНАЯ ПЕЧЬ
Размеры печи, мм: длина — 1020, ширина — 640, высота — 2380 (рис. 203). При одной топке в сутки теплоотдача, составляет 2000 ккал/ч, при двух — 3000 ккал/ч. Работает на угле. Топливник печи футеруют огнеупорным кирпичом на ребро, но так, чтобы он не подпирал кладку перекрытия (разрыв должен составлять не менее 30 мм). Дело в том, что коэффициенты расширения красного и огнеупорного кирпича неодинаковы.
Для кладки печи необходимы: красный кирпич — 420 шт., огнеупорный — 95 шт., песок, глина, огнеупорная глина — 0,05 м3, топочная дверца размером 210X250 мм, одна поддувальная и две прочистные дверцы 130X130 мм, колосниковая решетка250X300 мм, проволока, гвозди.
КУХОННЫЕ ПЛИТЫ
Кухонные плиты, или кухонные очаги, широко используют для приготовления, пищи, нагревания воды, отопления различных помещений, запарки кормов для скота, сушки грибов и различных продуктов, сушки одежды и т. д. Теплоотдача плит бывает разная и зависит от их размера, чаще всего не превышает 900 ккал/ч.

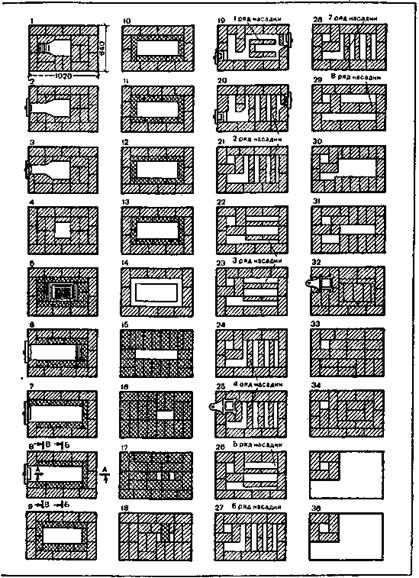
Рис. 203. Отопительная прямоугольная печь
Плиты рассматриваемых нами размеров, имеют небольшую массу — до 750 кг, их часто ставят прямо на полу, при условии, что он прочен и доски не прогибаются во время хождения. Лучше все же устроить под плиту фундамент.
При кладке очага надо учитывать размеры имеющихся чугунных плит и духовок, а также и водогрейных коробок, Если плиты изготовляются промышленностью, то духовки и .водогрейные коробки приходится изготовлять самим. Кровельную сталь для духовок надо брать толщиной не менее 1 мм. Толще сталь — долговечнее срок службы. Кроме того, необходимы колосниковые решетки, дверцы, задвижки, вьюшки и другие печные приборы.
Чтобы плита хорошо работала, необходимо при ее кладке тщательно соблюдать все размеры, особенно газоходов или каналов.
Кухонные плиты, выполняемые из кирпича, бывают разных конструкций и размеров, некоторые из них показаны на рисунке 204.
Для этих плит требуются: топочные дверцы размером 250X210 мм, поддувальные, прочистные дверцы и задвижки размером 130X130 мм, колосниковые решетки 250X180 мм, глина — в среднем 3 — 4 ведра, песок — 2 — 3 ведра.
Эти плиты подключают или к каким-либо печам или же к отдельно стоящим дымоходам.



Рис. 204. Кухонные плиты:
а — кухонная плита с духовкой; б — кухонная плита с духовкой, обогреваемой равномерно со всех сторон; в — кухонная плита с духовкой и водогрейной коробкой; 1 — чистка; 2 — водогрейная коробка; 3 — духовка; 4 — топливник; 5 — поддувало; £ — глиняная смазка толщиной 1 — 1,5 см; 7 — войлок, пропитанный глиняным раствором и покрытый кровельной сталью
Кухонная плита с духовкой
(рис. 204, а) размером 1020Х Х640 мм. Для выполнения требует 148 шт. кирпича.
Прежде всего на пол, по размеру печи, укладывают два слоя войлока, пропитанного глиняным раствором, и покрывают его кровельной сталью.
Первый ряд кладут сплошным, строго по угольнику, чтобы углы были 90°. Наружные стороны кладки могут быть выполнены из целого кирпича с заполнением середины половинками и четвертками.
Второй ряд целесообразно выложить из целого кирпича, но можно и из половинок, под чистку следует положить целый кирпич. Во время кладки надо соблюдать перевязку швов.
Третий ряд выкладывают согласно порядовке с оставлением места (колодца) для чистки. Если ее закрывают дверцей, то дверцу устанавливают, опирая на второй ряд, и закрепляют.
Четвертый ряд кладут согласно порядовке и с соблюдением указанных размеров, перевязкой швов и установкой поддувальной дверцы и ее закрепления. Зольник, поддувала делают шириной 190 мм (см. разрез по А — Л). У места присоединения плиты к дымоходу угол кирпича с внутренней стороны стесывают, лучше — закруглить.
Пятый ряд кладут, как показано на рисунке. Черная линия в виде рамки указывает то место, где будет установлена духовка с отступом от стенки с левой стороны на 100 мм.
Стенка для опирания духовки может быть выполнена из одного кирпича в четвертом ряду, поставленного на ребро.
Шестой ряд кладут согласно порядовке с установкой духовки и постановкой стенки в четверть кирпича с опиранием его на ранее поставленный на ребро кирпич. Это необходимо для образования канала между кирпичной кладкой и духовкой. Ранее выложенный канал над поддувалом сужают для того, чтобы на него можно было уложить колосниковую решетку.
Седьмой ряд кладут, как показано, с установкой колосниковой решетки (кладут на шестой ряд), со стесыванием кирпича на конус для того, чтобы топливо скатывалось на решетку, и выкладыванием стенки между топливником и духовкой из кирпича на ребро.
Восьмой и девятый ряды кладут согласно порядовкам, только в восьмом ряду ставят топочную дверцу.
Десятый ряд выкладывают, как показано, с перекрытием канала, идущего между духовкой и задней стенкой, применяя для этого целый кирпич и трехчетвертки. Перегородка должна быть выполнена на уровне духовки или выше ее на 10 — 15 мм. Со стороны топки ребро перегородки должно быть стесано на конус, а лучше — закруглено. Остается только канал с левой стороны печи.
Одиннадцатый ряд закладывают, как показано. Он образует как бы колодец, перекрывает духовку и топку и остается канал с левой стороны. Затем верх духовки смазывают глиняным раствором слоем в 10 — 15 мм, предохраняя ее от быстрого прогорания. Вообще толщина этой смазки должна быть такова, чтобы между смазкой и уложенным чугунным настилом из пяти составных плит 530X180 мм было пространство не менее 70 мм. Этот ряд необходимо выкладывать как можно ровнее, так как на него будет уложен чугунный настил.
Двенадцатый ряд является завершающим. Кладку не производят, а только укладывают чугунный настил на тонком слое глиняного раствора так, чтобы одна из конфорок находилась под топкой. На кладку этого ряда для прочности укладывают фаянс, т. е. надевают рамку из угловой стали, стягивая уложенные кирпичи.
Кухонная плита с духовкой, обогреваемой равномерно со всех сторон(рис. 204,6). У вышерассмотренной кухонной плиты стенка, имеющаяся между духовкой и топкой, плотно примыкает к одной стороне духовки и меньше нагревается. Подобный недостаток устранен у этой плиты.
Плита небольшого размера — 940X550 мм, без водогрейной коробки, перекрывается цельной плитой, а не настилом из отдельных плит. Если очаг будет примыкать к кирпичной стене или отопительному щитку, то заднюю стенку можно выполнять в четверть кирпича. Так как колоть кирпич не всегда удобно, то чаще стенку кладут в пол кирпич а.
Стоит этот очаг не прямо всей массой на основании или полу, а приподнят на два ряда кладки, примерно на 140 мм. Это делают с противопожарной целью. Поэтому кладку двух нижних рядов выполняют в виде каналов.
При кладке плиты колосниковую решетку ставят ниже порога топочной дверцы. Под должен иметь скаты к ней как спереди, так и сзади. Высота топки от колосниковой решетки до чугунной плиты или чугунного настила — около 200 мм.
Топка в основном рассчитана на дрова, но можно применять и другие виды топлива. Для каменного угля топка может быть высотой 160 — 180 мм. Для сжигания хвороста и различных сельскохозяйственных отходов топку делают более высокой (280 — 350 мм). Для кладки печи требуется: кирпича — 130 шт., глины — 3 ведра, песка — 2 ведра, цельная чугунная плита размером 762X456 мм с двумя конфорками, духовкой размером 320X270X400 мм (ширина, высота, глубина), колосниковая решетка 250X180 мм, поддувальная и топочные дверцы 220X160 мм, прочистная дверца 150Х110 мм и задвижка 130X130 мм. В зависимости от того, куда подключают плиту, можно ставить две задвижки.
Пространство между стенкой и духовкой имеет важное значение. Его можно устраивать в плите любой конструкции, только удлиняя ее размеры на 40 — 50 мм, т. е. на ширину промежутка, оставив размеры каналов, указанные в порядовках без изменения.
Первый ряд кладки выполняют размером 840X500 мм так, как показано в порядовке.
Второй ряд кладут аналогично, но с перекрытием среднего канала целым кирпичом, чтобы в дальнейшем обеспечить лучшую перевязку швов кладки.
Третий ряд кладки несколько больших размеров, чем второй, — 940X550 мм, с напуском над предыдущим рядом во все стороны на 50 мм.
Четвертый ряд выкладывают согласно порядовке. Средний кирпич стесывают, чтобы расширить выход канала к дымоходу. На рисунке (разрез В — В) и порядовке этот кирпич заштрихован, а выход газа показан стрелкой.
Пятый ряд кладут с установкой дверец для чистки и поддувала с закладкой отверстия кирпичом так, чтобы при необходимости его можно было свободно вынуть. В этом же ряду внутрь канала выпускают кирпич, который необходим как основание для установки духовки и кладки стенки в виде столбика для образования в дальнейшем вертикального канала между духовкой и правой боковой стенкой. Направление газов при выходе из-под духовки в дымоход показано стрелками. Для лучшего прохождения газов края кирпича под духовкой скашивают — закругляют.
В шестом ряду канал, выходящий к дымоходу, перекрывают, а кладку ведут так же, как в пятом ряду.
В седьмом ряду устанавливают духовку от правой стенки с отступом 90 мм, а от левой перегородки — 40 мм. Поддувало перекрывают. Кладку ведут так, как показано на рисунке.
Восьмой ряд кладут согласно порядовке, с уменьшением отверстия над поддувалом.
Девятый ряд кладут, как показано, с установкой колосниковой решетки и топочной дверцы. В этом ряду заканчивают кладку перегородки между духовкой и топкой.
В десятом ряду перекрывают отверстие между перегородкой и духовкой и канал, расположенный между духовкой и задней стенкой. Остается открытым только канал с правой стороны.
Одиннадцатый ряд кладут, как показано. Кирпич, укладываемый на перегородку, стесывают со стороны топки или укладывают под углом, как показано в разрезе А — Л. Верх духовки смазывают глиняным раствором толщиной 10 — 15 мм, чтобы между духовкой и уложенной чугунной плитой было пространство или канал высотой 70 мм.
Двенадцатый ряд — завершающий. На глиняном растворе укладывают двухконфорочную плиту и ставят фаянс — обвяз из угловой стали,
Кухонная плита с духовкой и водогрейной коробкой (рис. 204,б).
Размеры плиты 1150X640 мм. Для устройства необходимы: кирпич — 185 шт., глина — 4 ведра, песок 2 — 3 ведра, топочная дверца размером 250X210 мм, поддувальная и прочистная дверцы 130X130 мм, одна или две дымовые задвижки 130X130 мм, колосниковая решетка 250X180 мм, пять чугунных составных плит 530X180 мм с двумя конфорками, духовой шкаф 350X350X450 мм и водогрейная коробка 350X150X450 мм.
Первый ряд кладут по размеру и строго по угольнику, чтобы углы были 90°. Наружные стороны кладки могут быть выполнены из целого кирпича с заполнением середины половинками и четвертками.
Во втором ряду наружные стороны и место для чистки лучше выложить из целого кирпича. Для внутренней кладки можно использовать половинки и четвертки. Третий ряд кладут из целого кирпича. Под духовкой устраивают чистку и ставят дверцу.
Четвертый ряд выполняют по порядовке. В этом ряду ставят перегородки из кирпича на ребро с отступом от задней стенки на 70 — 80 мм и от внутренней — на 130 мм. Отверстие в задней стенке для устройства дымохода должно быть не менее 130 мм. Угол кирпича у отверстия скашивают на конус для обеспечения более плавного движения газов. В этом ряду устанавливают дверцу для поддувала.
Пятый ряд кладут, как четвертый. В этом ряду показано пунктирными линиями местоположение водогрейной коробки, духовки с оставлением между ними канала шириной 80 — 90 мм.
Шестой ряд кладут согласно порядовке. Здесь на тонком слое глиняного раствора устанавливают и закрепляют духовой шкаф и водогрейную коробку с расстоянием между ними 80 — 90 мм, необходимым для устройства вертикального канала. По каналу будут проходить горячие газы, нагревая духовку и водогрейную коробку, которые к тому же подняты над третьим -рядом кладки на 140 — 150 мм, образуя горизонтальный нижний канал. Пространство у задней стороны шкафа и коробки, т. е. между их боковыми стенками, закладывают кирпичом, создавая перегородку сечением 80X80 или 90X90 мм, высотой 250 мм.
При устройстве такой перегородки образуется канал шириной 70 — 80 мм, длиной 500 мм, через который будут выходить горячие газы в дымоход.
В седьмом ряду над поддувалом ставят колосниковую решетку так, чтобы она была ниже уровня топочного отверстия не менее чем на один ряд кладки (65 — 75 мм). Поду топливника придают форму корыта, стесывая кирпич по его широкой стороне (см. разрез по В — В). Решетку своими прорезями кладут по длине топливника с уклоном к дверце на 20 — 30 мм. Духовой шкаф со стороны топки до самого верха облицовывают кирпичом на ребро, чтобы предохранить его стенку от быстрого прогорания и чрезмерного нагревания.
Восьмой и девятый ряды кладут так, как показано в порядовках.
В десятом ряду задний канал перекрывают примерно трехчет-вертками так, чтобы они вплотную примыкали к шкафу, перегородке и коробке. В этом ряду заканчивают облицовку, стенки духового шкафа. Верхнюю часть облицовки, т. е. кирпич, стесывают на фаску, а еще лучше закругляют (см. разрез по А — А).
Одиннадцатый ряд кладут, как показано, с закрытием верха водогрейной коробки и оставлением только одного вертикального канала между коробкой и духовкой. Духовку сверху смазывают глиняным раствором.
Двенадцатый ряд — завершающий. Укладывают чугунный настил на глиняном растворе. Для прочности верхний ряд окаймляют с трех или четырех сторон из угловой стали сечением от 25X25X3 до 40X40X3 мм.
Перед топками всех печей прибивают подтопочные листы из кровельной стали, с предварительной укладкой на пол листового асбеста или войлока, смоченного в глиняном растворе.
Окончив кладку, из чисток удаляют весь упавший глиняный раствор и заделывают их кирпичом на глиняном растворе.
Очаги массой до 750 кг ставят на прочных деревянных полах. При большей массе под них подводят фундамент, который требуется и для устройства отдельной дымовой трубы.
УХОД ЗА ПЕЧАМИ И ИХ РЕМОНТ
Если печи топят постоянно, то их чистят 2 раза в год — весной и осенью. Печи, которые топят только зимой, чистят лишь осенью. Удаление сажи необходимо, чтобы повысить тягу в печах и обеспечить лучшее нагревание стенок. После чистки нужно осмотреть печи и замазать все имеющиеся в них, даже мельчайшие, трещины, потому что в эти трещины подсасывается воздух и охлаждает нагретые стенки.
Особенно тщательно следует замазывать трещины около различных дверец, так как подсос воздуха через них очень сильно охлаждает печь.
Следует также осматривать трубы на чердаке, так как от их неисправности возникают пожары. Чтобы на них были заметны даже самые мелкие трещины, трубы необходимо побелить известью или мелом. На белом фоне быстро замечается появление копоти. Для ремонта печей используют глиняный раствор. Ремонтируемые места следует хорошо смочить водой, нанести глину и тщательно загладить ее.
Образованию конденсата способствует быстрое остывание трубы. Чтобы утеплить трубу, ее можно оштукатурить известково-гипсовым раствором слоем не менее 20 — 25 мм. Более теплый раствор получается от применения шлакового песка, просеянного на частом сите (3X3 м). Оштукатуренные трубы следует также систематически осматривать. Верхнюю часть трубы, или оголовок, нужно оштукатуривать известково-цементным или цементным раствором.
Утепляя трубы, их можно облицовывать гипсошлаковыми или цементно-шлаковыми плитами нужных размеров, толщиной 50 — 70 мм. Плиты ставят вокруг трубы, скрепляют проволокой, промазывают швы глиняным, известковым или гипсовым раствором.
Изготавливают плиты также толщиной 20 — 30 мм, но такого размера, чтобы их можно было установить от трубы на расстоянии 50 — 70 мм, а швы промазать. Таким образом, между трубой и плитами остается воздушная прослойка или пространство. Это пространство засыпают сухим котельным шлаком или другим легким несгораемым материалом. Материалы просеивают через сито с ячейками не реже 5X5 мм.
Вместо плит можно применять любой листовой металл, изготовляя из него короба или футляры, состоящие из двух или четырех частей, которые крепят вокруг трубы на некотором расстоянии от нее, а пространство засыпают. Для предохранения черной стали от ржавления ее окрашивают два раза масляной или другой краской. Воздушную прослойку в чистом виде или с засыпкой под кровлей закрывают плитками или кирпичом, но только не деревом и промазывают швы.
Рекомендуется не реже одного раза в год облицовку снимать, осматривать трубы и, если нужно, ремонтировать.
ВОДЯНОЕ ОТОПЛЕНИЕ
В сельской местности, рабочих и дачных поселках дома часто отапливают при помощи самостоятельного генератора тепла — котла небольшого размера.
Наиболее надежным и простым считается водяное отопление, топливом для которого могут служить каменный уголь, дрова, разного рода брикеты, природный газ, керосин, соляровое масло и т. д.
Для оборудования водяного отопления необходимы котел, нагревательные приборы (радиаторы), трубы, расширительный сосуд, запорно-регулирующая арматура (краны, вентили). Все это продается в специализированных магазинах.
Во всех случаях котел должен быть экономичным, т. е. потреблять как можно меньше топлива и выделять больше тепла.
Устанавливать котлы надо как можно ближе к жилым комнатам (например, в кухне), но так, чтобы не ухудшались санитарно-гигиенические условия квартиры. Если котел представляет собой радиаторы, вмонтированные в кухонную плиту, то его лучше облицевать изразцами.
Установив котел, от него отводят трубы к нагревательным приборам — радиаторам или регистрам. Регистры сваривают из нескольких труб нужного диаметра. Вверху генератора ставят расширительный сосуд.
Нагретая вода из котла по трубам направляется в нагревательные приборы, которые отдают тепло отапливаемым помещениям. Горячая вода, нагревая приборы, охлаждается и по другому ряду труб (трубопроводу) поступает обратно в генератор тепла.
От котла к приборам вода движется за счет разности объемных весов воды; более легкой горячей и более тяжелой охлажденной.
Вот почему котел в системах квартирного отопления рекомендуется располагать по возможности ниже нагревательных приборов. Это повышает циркуляционное давление в системе, позволяет выбрать меньшее сечение труб.
Если котел нельзя поставить ниже нагревательных приборов, то его располагают на одном уровне с ними или чуть выше. При такой установке вода циркулирует исключительно за счет своего охлаждения в трубопроводах. Чем больше она охлаждается, тем сильнее циркуляция, и наоборот.
Трубы системы должны быть открыты; изолируют лишь главный стояк, идущий от котла, причем только в пределах помещения, в котором расположен котел. Если не изолировать стояк, в помещении будет очень жарко.
СИСТЕМЫ ОТОПЛЕНИЯ
Наиболее распространенной является система двухтрубного водяного отопления с прокладкой горячей разводящей линии под потолком помещения и обратной линии у пола под нагревательными приборами (рис. 205).

Рис. 205. Схема квартирного водяного отопления с прокладкой горячей линии под потолком, а обратной у пола:
1 — раковина; 2 — переливная воздушная линия от расширителя; 3 — расширительный сосуд; 4 — горячая разводящая линия; 5 — главный стояк; 6 — генератор тепла (котел); 7 — водопровод для наполнения и подпитки системы водой; 8 — спуск воды из системы; 9 — обратная линия; 10 — нагревательные приборы
Котел, в зависимости от конструкции, устанавливают отдельно или встраивают в печь (если он имеет вид змеевика из труб или радиатора).
От котла вверх идет главный стояк, на котором располагают расширительный сосуд (бак), рассчитанный на увеличение объема воды при ее нагревании. В зависимости от кубатуры помещения общий объем бака колеблется от 20 до 45 л, а полезный — от уровня подключения горячей магистрали к сосуду до уровня переливной (воздушной) трубы. Форма бака может быть различной. Изготовляют его из листовой 2 — 3-миллиметровой стали и отрезка трубы большого диаметра. Внутри и снаружи его окрашивают масляной краской, сверху закрывают крышкой. К баку подключают переливную трубу или воздушную линию без вентиля. Это необходимо для того, чтобы расширившаяся при нагревании вода не выливалась на пол, а направлялась в канализацию. На расширительном сосуде (баке) желательно укрепить указатель уровня воды. Ниже бака от главного стояка прокладывают линию горячей воды, а от нее — отдельные трубы на один или два прибора.
От водопровода к котлу проводят линию с запорным вентилем, необходимую для заполнения и пополнения системы водой. Для спуска воды из системы также имеется патрубок с вентилем, который можно подсоединить к канализации.
Отсутствие водопровода в доме не мешает оборудованию водяного отопления, поскольку наполнять систему водой приходится очень редко. Наполнять ее можно ручным насосом или из ведра, устроив для этого в крышке расширителя отверстие, закрываемое пробкой.
Расширитель лучше всего ставить в отапливаемом помещении; иногда его ставят и на чердаке, но при этом хорошо утепляют и оборудуют циркуляционной линией для предотвращения замерзания воды.
Прокладывать горячую и обратную линию рекомендуется с уклоном 3 — 5 мм на 1 пог. м трубопровода с направлением в сторону движения воды. Это обеспечивает свободный выход воздуха через переливную трубу, идущую от расширителя, и спуск воды через патрубок, расположенный в нижней точке системы.
На схеме рисунка 205 видно, что обратный трубопровод проходит над полом. Однако такая прокладка не всегда возможна (мешают двери, перегородки), поэтому трубы иногда приходится прокладывать под полом.
Вместо этого варианта допустима прокладка обратного трубопровода рядом с горячим, идущим под потолком помещения (рис. 206). Система работает следующим образом. Из котла горячая вода поступает в нагревательные приборы. Здесь она охлаждается и по обратной линии под потолком попадает в нагревательный котел. Чтобы воздух выходил из обратной линии, последняя соединяется в верхней точке петлей, выгнутой из трубы, с воздушным пространством расширителя.
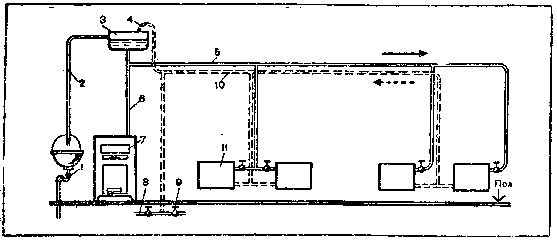
Рис. 206. Схема квартирного водяного отопления с прокладкой горячей и обратной линии под потолком:
1 — раковина; 2 — переливная воздушная линия; 3 — расширительный сосуд; 4 — воздушная петля; 5 — горячая разводящая линия; 6 — главный стояк; 7 — генератор тепла (котел); 8 — патрубок с вентилем для спуска воды из системы; 9 — водопровод для наполнения и подпитки системы водой; 10 — обратная линия; 11 — нагревательные приборы
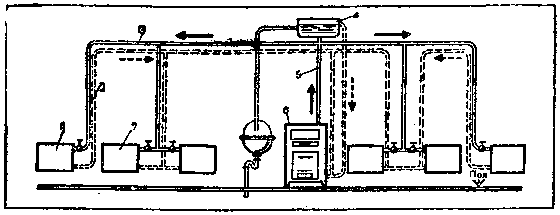
Рис. 207. Схема квартирного водяного отопления с прокладкой горячей и обратной линии над приборами:
1, 7 — нагревательные приборы; 2 — обратная линия; 3 — горячая разводящая линия} 4 — - расширительный сосуд; 5 — главный стояк; 6 — генератор тепла (котел)
Недостаток рассмотренной системы — наличие нескольких циркуляционных колец. Из-за этих колец вода в обратном стояке иногда остывает, и циркуляция прекращается.
Более совершенная, но и более сложная схема отопления приведена на рисунке 207. Особенностью ее является то, что охлажденная вода направляется не сразу вверх и в котел, а вниз, где смешивается с водой, поступающей от расширителя, и затем уже по общему трубопроводу направляется в котел.
В этой системе холодная вода от нагревательных приборов, установленных вдали от котла, смешивается с теплой, поступающей от более близких к котлу приборов, не в верхних, а в нижних трубах. В результате понижение температуры воды в обратной линии способствует ее ускоренному движению, т. е. улучшению циркуляции.
При монтаже системы отопления перед каждым нагревательным прибором от основной горячей линии ставят вентиль, которым регулируют количество подаваемой воды в приборы, т. е. повышается или понижается температура в комнатах.
Отопление может монтировать или сам застройщик, если он знаком с санитарно-техническими работами, или слесарь-сантехник.
ГЕНЕРАТОРЫ ТЕПЛА (КОТЛЫ)
Генераторы тепла (котлы) для квартирных систем изготовляют из чугуна, стали или другого материала, могут работать на твердом, жидком или газообразном топливе. Их можно устанавливать изолированно или в комбинации с кухонной плитой,
В настоящее время промышленность выпускает котлы разных конструкций. Особенно широкое применение нашли секционные чугунные котлы типа КЧМ:1, выпускаемые Кировским чугунолитейным заводом и Каунасским заводом сантехнических изделий. Разработано семь моделей этого котла с количеством секций от 4 до 10 и поверхностью нагрева от 1,31 до 3,65 м2. Квадратный метр поверхности нагрева котла выделяет 10000 ккал/ч; КПД — 65 — 70%. Топливо — высококалорийный сортированный каменный уголь, кокс, брикеты или газ. Топку загружают углем через 3 — 6 ч, чистят один раз в сутки с последующим разжиганием новой порции топлива. Рабочее давление котла — 2 атм с максимальной температурой нагрева воды 95°С.
Подбирают котел на основе специального расчета, по паспортным данным, по наружному объему здания.
Для котла КЧМ-1 эти данные имеют следующий вид:
| Строительный объем здания, м3 | ||||
| Количество секций котла, шт. | ||||
| Поверхность нагрева котла, м2 | 1,31 | 1.73 | 2,06 | 2,48 |
| Теплопроизводительность котла, ккал/ч | ||||
| Длина котла, м | 0,340 | 0,425 | 0,510 | 0,595 |
| Масса котла номинальная, кг | ||||
| Высота котлов всех размеров, м | 1,032 | |||
| Ширина котлов, м | 0,45 |
Котлы КЧМ-2 изготовляет Каунасский завод сантехнических изделий в собранном виде, разной теплопроизводительности и массы; площадь нагрева: 1,67; 2,11; 2,5; 2,95; 3,39; 3,83; 4,23 м2. Теплопроизводительность котлов — от 17000 до 45000 ккал/ч, длина — от 345 до 885 мм, высота — 1040 и ширина — 450 мм, Масса котлов — от 278 до 539 кг. Стоимость — от 115 до 199 руб.
Котел КЧММ выпускает опытное производственное предприятие «Энерготехпром» Министерства энергетики и электрификации СССР в собранном виде. Этот котел состоит из трех секций, покрытых кожухом и снабженных всей необходимой гарнитурой. Поверхность нагрева — 1,05 м2, вместимость котла — 9,54 л, производительность — не менее 10000 ккал/ч. Размеры котла, мм: длина — 390, ширина — 375, высота — 860. Масса котла — 143,5 кг. Цена в собранном виде — 85 руб.
Котлы КЧММ-2 выпускает Московский чугунолитейный завод имени П. Л. Войкова с площадью нагрева: 0,9; 1,0; 1,44 м2, тепло-производительностью 9000, 12000 и 15000 ккал/ч, соответственно массой 150, 172 и 192 кг. Длина — 590, 670 и 755 мм, ширина — 450, высота — 680 мм. Стоимость котлов — от 81 до 95 руб.
Котел-плиту КВП-0,92 выпускает завод «Волгоцеммаш» в городе Тольятти Куйбышевской области.
Котел-плита предназначен для отопления жилых помещений общей площадью не более 75 м2 и одновременного подогрева пищи. Поверхность нагрева — 0,92 м2, Теплопроизводительность — 10000 ккал/ч. Размеры котла, мм: высота — 880, ширина — 505, длина 610 с топкой объемом 0,05 м3. Масса котла — не более 130 кг. Розничная цена — 90 руб. Вместимость котла-плиты — 35 л. Отверстие конфорки — 185 мм. Работает котел на антраците, каменном угле, коксе, брикетированном малозольном топливе и дровах. Во время работы котла можно подогревать пищу, используя конфорку.
В котлах рассмотренных конструкций ограничены размеры топок, и они требуют частой добавки топлива, что создает определенные неудобства при пользовании ими. Поэтому весьма удобны котлы нижнего горения, с гравитационной топкой. Топливо загружается в котел под действием собственной массы; оно как бы сползает в очаг горения на колосниковую решетку. Толщина слоя топлива все время остается постоянной, а это весьма важно для нормального горения. Топливник загружают топливом на сутки или больше. В таких котлах имеется также мусоросжигающее устройство с отдельным бункером для горючего мусора. Это не только снижает расход топлива, но и удаляет часть мусора. Котлы с гравитационной топкой изготовляют с поверхностью нагрева от 5 до 12 м2, теплопроизводительностью — от 40000 до 96000 ккал/ч. Длина котлов — от 645 до 1520 мм, масса — от 1050 до 2100 кг.
Водогрейные котлы типа ВБК-12 выпускает электрогенераторный завод в городе Сарапул Удмуртской АССР. Котлы рассчитаны для обогрева помещений до 120 м2. Одной заправки каменным углем достаточно для того, чтобы он горел в течение 3,5 суток. Топливо в зону горения подается постепенно, по мере сгорания. Котел не требует тщательного ухода. Его ориентировочная стоимость — 200 руб.
Малогабаритные котлы пользуются большим спросом у населения, особенно у сельских новоселов.
Кроме котлов для квартирного отопления, применяют также огневоздушные нагреватели различных конструкций, изготовляемые из чугуна или стали. Обычно они состоят из внутренних элементов и наружного кожуха.
Эти воздухонагреватели имеют топливник и бункер для топлива. Горячие газы проходят по каналам воздухонагревателя, а затем в дымовую трубу, нагретый воздух направляется в каналы воздушного отопления. Для увлажнения подогретого воздуха в верхней части воздухонагревателя, над топливником, устанавливают бачок с водой. Поверхность нагрева и масса этих приборов бывают разные.
Печи-камины «Алма-Ата» выпускает Алма-Атинский завод «Электробытприбор». Печь-камин не только отлично обогревает жилые дома площадью до 40 м2, но и помогают быстро приготовить пищу. Металлический корпус, нагревая воздух, обеспечивает хорошую конвективную циркуляцию. Печь-камин «Алма-Ата» работает на любом жидком топливе, например керосине, к тому же она предельно проста и удобна в эксплуатации. К печи-камину прилагается топливный бак вместимостью 13 л. Эта печь экономна. Одного литра горючего хватает на 4 ч непрерывной работы. Теплопроизводительность печи — 6500 ккал/ч. Печь компактна и занимает мало места в доме. Ее размеры — 730Х560Х Х425 мм, масса — 45 кг, стоимость 68 руб.
Кроме рассмотренных отопительных приборов-котлов и всевозможных обогревателей, имеются и другие, выпускаемые различными предприятиями страны.
При установке котла пол следует тщательно изолировать слоем асбеста толщиной не менее 5 мм, а поверх него уложить листы кровельной стали. Вместо асбеста можно положить четыре (слоя войлока, смоченного в глиняном растворе.
Если достать котел невозможно, устраивают отопительно-варочные печи, представляющие собой сочетание котлов с плитами. Котлами в таких печах служат змеевик из газовых труб, несколько обычных радиаторов и т. д.

Рис. 208. Котел-плита конструкции К. А. Дмитриева со змеевиком (планы, разрезы и общий вид)
Существует несколько конструкций таких плит: Л. А. Семенова, А. В. Хлудова, В. М. Артюшенко, KЛB-2 и др. Широкое распространение получил котел-плита конструкции К. А. Дмитриева (рис. 208).
Удобна эта плита тем, что вода в ней нагревается как отводящими от плиты газами, так и при самостоятельном отоплении.
Плита, представляющая собой единое целое со змеевиком, .служит для отопления и горячего водоснабжения. Она имеет два «обособленных топливника (один — для плиты, другой — для змеевика), подключаемых к отдельным дымоходам. В теплое время года для горячего водоснабжения достаточно тех газов, которые поступают от топки плиты. В холодное время пользуются самостоятельным топливником.
Устроить змеевик можно из газовой дюймовой трубы (внутренний диаметр 25 мм) длиной не менее 7 м. Придав змеевику необходимую форму, его приваривают к верхнему и нижнему коллекторам, сделанным из газовой 2-дюймовой трубы. Поверхность нагрева змеевика — 0,8 м2, вместимость — 7,5 л, теплопроизводитель-ность — 8000 ккал/ч.
Котел-плита со змеевиком работает так. Из топливника для плиты горячие газы направляются сначала под плиту, затем — под духовой шкаф, а оттуда — в дымовую трубу. Соединенный с топливником котла последний газоход плиты в это время должен быть закрыт.
Горячие газы из топливника для обогрева змеевика сначала поднимаются вверх, омывают часть змеевика над топкой, попадают во второй газоход, опускаются вниз и уходят в дымовую трубу, построенную для топливника змеевика. В 2 м от пола (выше задвижки) оба дымовых канала могут работать независимо друг от друга.
Если змеевик необходимо обогревать горячими газами, идущими от плиты (что допустимо при температуре наружного воздуха до — 5°, когда в помещении приходится поддерживать небольшую температуру), то эти газы сначала направляют под змеевик, а затем — в дымовую трубу, предназначенную для котла. Для этого задвижку за плитой закрывают, а за котлом открывают. Должна б
Последнее изменение этой страницы: 2016-07-23
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...