
Главная Случайная страница
Категории:
ДомЗдоровьеЗоологияРнформатикаРскусствоРскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиРкологияРРєРѕРЅРѕРјРёРєР°Рлектроника
Базовые конструкции языка программирования Pascal.
Р‘РЛЕТ в„–1
Базовые конструкции языка программирования Pascal.
В 1966г. Дейкстра опубликовал структурную теорему. Любую программу можно написать с помощью 3х базовых структур:
· следование;
· ветвление;
· обобщённый цикл.
Следование
Команды идут друг за другом.
Ветвление (развилка)
Если в программе должен быть нарушен естественный ход, то выполняется структура ветвления. Структура реализуется с помощью условных операторов, эта конструкция имеет полный (по каждому условию выполняются действия, после чего ветви соединяется) и неполный вид (выполняется действие лишь по одной ветви, после чего ветви соединяются).
Условный оператор Ifобеспечивает выполнение или невыполнение некоторых операторов в зависимости от соблюдения определённых условий. Формат:
if <условие> then <оператор1> [else <оператор2>];
Если условие истинно, то выполняется оператор1, в противном случае выполняется оператор2. Оба оператора м.б. составными.
Обобщенный цикл
Оператор Whileчасто называют оператором цикла с предусловием за то, что проверка условия выполняется перед телом цикла и производится в самом начале оператора.
While <условия продолжения повторений> do <тело цикла>;
Оператор повтора Repeat аналогичен оператору While, но отличается от него, во-1х, тем, что условие проверяется после очереди выполнения операторов тела цикла, а во-2ых, тем, что критерием прекращения цикла является равенство условия выражения True. За это цикл Repeat называют циклом с постусловием, или циклом «ДО». Repeat состоит из заголовка repeat, тела и условия окончания until.
Repeat <оператор1> . . . <операторN>
Until <условие окончания цикла>;
Оператор повтора For.Число повторений задается переменной, называемой параметром цикла, или управляющей переменной. Оператор повтора Forсостоит из заголовка и тела цикла.
For <параметр цикла> : = <S1> to <S2> do <оператор>;
Предмет РњРџР, его цели Рё задачи.
Методика преподавания информатики направлена на разработку методов, позволяющих учителю проводить обучение на высоком уровне и достигать максимальной эффективности при минимальной затрате сил и ресурсов для достижения результата. В этом смысле методика преподавания чем-то сродни экономике. Т.к. методика является частью педагогики, то учитель может опираться на уже известные педагогические приемы, однако при этом необходимо учитывать специфичность самой дисциплины информатики. Поэтому МПРнемыслима без психолого-педагогических исследований, к.т. должны включать разработку теоретико-практических основ построения учебной деятельности с учетом машинного и безмашинного вариантов обучения. МПРпредставляет собой науку, аккумулирующую в себе достижения педагогики, психологии, философии.
Предмет МПРделится РЅР° РґРІРµ части: первая включает РІ себя РІРѕРїСЂРѕСЃС‹ общей методики Рё вторая частной методики. Назначение первой части – дать общее представление Рѕ предмете исследования РњРџР, С‚.Рµ. РѕР± информатике, Рѕ проблемах связанных СЃ преподаванием этой дисциплины Рё возможных путях Рё средствах разрешения этих проблем. Назначение второй части – ознакомить СЃ некоторыми методическими приемами РїСЂРё изложении отдельных тем.
Термин «методика» произошел от греческого «methodos», что значит путь исследования теории, учения, способ достижения какой-то цели. Цель -это идеальное мысленное предвосхищение результата деятельности.
Основные цели РњРџР:
· разработка концепции преподавания информатики;
· разработка учебных программ по информатике, реализующих принятую концепцию. Одни учебные программы должны соответствовать реальному уровню информатизации в регионе, стране, а другие могут включать в себя пункты, учитывающие перспективы создания и внедрения новых информационных технологии.
· вооружение учителя информатики знаниями, умениями и навыками, необходимыми для рационального и творческого преподавания предмета в школе, проведения внеклассной работы.
Как и каждая методическая система любой другой школьной дисциплины МПРнацеливает учителя на решение следующих задач:
· воспитательной
· общеобразовательной
· развивающей.
3.Заполнить таблицу размерности n*n:
1 2 3 … n
1 2 3 … n
……….
1 2 3 … n
program lab4;
type mas=array[1..100, 1..100] of integer;
var a:mas;
i,n,j:integer;
begin
writeln('Vvedite n');
readln(n);
for i:=1 to n do
for j:=1 to n do
a[i,j]:=j;
for i:=1 to n do
begin
for j:=1 to n do
write(a[i,j],' ');
writeln;
end;
end.
Р‘РЛЕТ в„–2
Задан некоторый набор товаров. Определить для каждого из товаров, какие из них имеются в каждом магазине и каких товаров нет ни в одном магазине.
program lab1;
const N=3;
type product = (bread, butter, cheese, milk);
assortiment = set of product;
stor = array[1..n] of assortiment;
var
m1:stor;
x:product;
a,b,c,xm1:assortiment;
i,j,iw,m:integer;
begin
for i:=1 to n do
begin
xm1:=[];
writeln('enter the number of product',i:2,'stor');
repeat
writeln('1: x:=bread; 2: x:=butter; 3: x:=cheese; 4: x:=milk; 5: break');
writeln('Vvedite 1 or 2 or 3 or 4 or 5');
read(iw);
case iw of
1: x:=bread;
2: x:=butter;
3: x:=cheese;
4: x:=milk;
5: break;
end;
xm1:=xm1+[x];
until iw=5;
m1[i]:=xm1;
end;
a:=m1[1];
c:=[bread..milk];
for i:=1 to n do
begin
b:=b+m1[i];
a:=a*m1[i];
c:=c-b;
end;
for i:=1 to 2 do
begin
case i of
1:writeln('products are in all stors:');
2:writeln('products arent in all stors:');
end;
for x:=bread to milk do
if x in a then
case x of
bread:writeln('bread');
butter:writeln('butter');
cheese:writeln('cheese');
milk:writeln('milk');
end;
if i=1 then a:=c;
end;
end.
Р‘РЛЕТ в„–3
1. Алгебра высказываний как модель алгебры Буля, ее аксиоматическое задание. Принцип двойственности и теорема двойственности.
Высказыванием называется законченное повествовательное предложение, для кото-рого можно сказать истинно оно или ложно. Высказывание не м/б одновременно и истинным, и ложным.
Высказывания бывают атомарные (неделимые), или элементарные, исходные и сложные (составные).
РР· элементарных высказываний СЃ помощью операций над высказываниями или логических СЃРІСЏР·РѕРє строят сложные высказывания.
Операции над высказываниями:
1. Операция конъюнкции ( /\ ).
Конъюнкцией двух высказываний, А и В, называется новое высказывание, обозначаемое (A /\ B), которое истинно тогда и только тогда, когда высказывания A и B истинны одновременно, и ложно во всех остальных случаях. Конъюнкции соответствует логическая связка "и".
2. Операция дизъюнкции ( \/ ).
Дизъюнкцией двух высказываний, А и В, называется новое высказывание, обозначаемое (A \/ B), которое истинно только тогда, когда истинно, по крайней мере, одно из высказываний, A или B, и ложно в единственном случае, когда оба высказывания, А и В, ложны. Дизъюнкции соответствует связка "или".
3. Операция следования или импликации ( → )
Рмпликацией (следованием) РґРІСѓС… высказываний, Рђ Рё Р’, называется РЅРѕРІРѕРµ высказывание, обозначаемое (A → B), которое ложно тогда Рё только тогда, РєРѕРіРґР° A - истинно, Р° B - ложно, РІРѕ всех остальных случаях высказывание (A→B) истинно. Р’ высказывании (A → B) A - называется посылкой или антецедентом, B - следствием или консеквентом. Рмпликация (A → B) РІ разговорной речи имеет несколько разночтений: если A, то B;РёР· A следует B;A влечет B;B следует РёР· A;A достаточно для B;B необходимо для A.
4. Операция эквивалентности ( ↔ )
Рквивалентностью РґРІСѓС… высказываний, A Рё B, называется РЅРѕРІРѕРµ высказывание, обозначаемое (A ↔ B), которое имеет значение ложь тогда Рё только тогда, РєРѕРіРґР° A - истинно, Р° B - ложно или A - ложно, Р° B - истинно. Рђ значение истина тогда Рё только тогда, РєРѕРіРґР° одновременно РѕР±Р° высказывания, A Рё B, либо истинны, либо ложны. Рквивалентность (A ↔ B) РІ разговорной речи имеет несколько разночтений: A необходимо Рё достаточно для B; A тогда Рё только тогда, РєРѕРіРґР° B; A эквивалентно B; A равносильно B; РёР· A следует B , Р° РёР· B следует A.
5. Операция отрицания() Отрицанием высказывания A называется новое высказывание, обозначаемое  , которое истинно тогда и только тогда, когда ложно A, и ложно тогда и только тогда, когда A истинно.
, которое истинно тогда и только тогда, когда ложно A, и ложно тогда и только тогда, когда A истинно.
Алгеброй Буляназывается непустое множество, содержащее, по крайней мере, два элемента и замкнутое относительно 2-ух бинарных операций: /\ и \/, удовлетворяющих законам: коммутативности (1), ассоциативности (2), дистрибутивности конъюнкции относительно дизъюнкции и дизъюнкции относительно конъюнкции (3), идемпотентности (4), сокращения (5), поглощения (6), противоречия для конъюнкции и исключения третьего для дизъюнкции (7), законам де Моргана (8) и закону двойного отрицания (9).
1. 


2. 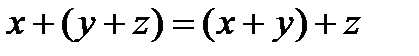
x * ( y * z ) = (x * y) * z
3. 
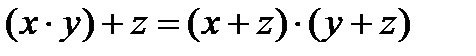
4. x * x = x
x + x =x
5. x * Р = x
x + Р› = x
6. x * Р› = Р›
x + Р = Р _
7. x * x = Р› _
x + x = Р
8. 
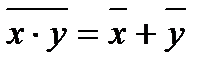
9. 
10. 
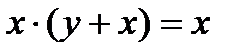
Доказательство.
По условию доказываемой теоремы:
β(X1, X2, ..., Xn). ≡ α(X1, X2, ..., Xn) (1).
РџРѕ условию теоремы 1: β*(  1,
1,  2, ...,
2, ...,  n) ≡ β
n) ≡ β 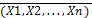 , откуда
, откуда
β*(  ,
, 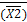 , ...,
, ..., 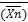 ) ≡ β
) ≡ β  , следовательно
, следовательно
β*(X1, X2, ..., Xn) ≡ β  (2).
(2).
Аналогично, α*(X1, X2, ..., Xn) ≡ α  (3).
(3).
РР· (1) следует, что β 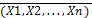 . ≡ α
. ≡ α 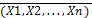 , откуда
, откуда
β  ≡ α
≡ α  (4). РџРѕ свойству равносильности [β*(X1, X2, ..., Xn) Рё α*(X1, X2, ..., Xn) равносильны соответственно выражениям β
(4). РџРѕ свойству равносильности [β*(X1, X2, ..., Xn) Рё α*(X1, X2, ..., Xn) равносильны соответственно выражениям β  Рё α
Рё α  , которые СЏРІР». равносильными] β*(x1, x2, ..., xn). ≡ α*(x1, x2, ..., xn), что Рё требовалось доказать.
, которые СЏРІР». равносильными] β*(x1, x2, ..., xn). ≡ α*(x1, x2, ..., xn), что Рё требовалось доказать.
Закон двойственности "наполовину уменьшает работу математикам": если уже доказана некоторая равносильность, то справедливость другой, полученной из первой двойственными преобразованиями, уже не нужно доказывать, она будет выполняться.
Р‘РЛЕТ в„–4
Р‘РЛЕТ в„–5
1. Рмитационное моделирование — метод, позволяющий строить модели, описывающие процессы так, как РѕРЅРё проходили Р±С‹ РІ действительности. Такую модель можно «проиграть» РІРѕ времени как для РѕРґРЅРѕРіРѕ испытания, так Рё заданного РёС… множества. РџСЂРё этом результаты Р±СѓРґСѓС‚ определяться случайным характером процессов. РџРѕ этим данным можно получить достаточно устойчивую статистику.
Рмитационное моделирование — это метод исследования, РїСЂРё котором изучаемая система заменяется моделью СЃ достаточной точностью описывающей реальную систему Рё СЃ ней проводятся эксперименты СЃ целью получения информации РѕР± этой системе. Ркспериментирование СЃ моделью называют имитацией (имитация — это постижение сути явления, РЅРµ прибегая Рє экспериментам РЅР° реальном объекте).
Рмитационное моделирование — это частный случай математического моделирования. Существует класс объектов, для которых РїРѕ различным причинам РЅРµ разработаны аналитические модели, либо РЅРµ разработаны методы решения полученной модели. Р’ этом случае математическая модель заменяется имитатором или имитационной моделью.
Рмитационная модель — логико-математическое описание объекта, которое может быть использовано для экспериментирования РЅР° компьютере РІ целях проектирования, анализа Рё оценки функционирования объекта.
Применение имитационного моделирования
К имитационному моделированию прибегают, когда:
· дорого или невозможно экспериментировать на реальном объекте;
· невозможно построить аналитическую модель: в системе есть время, причинные связи, последствие, нелинейности, стохастические (случайные) переменные;
· необходимо сымитировать поведение системы во времени.
Цель имитационного моделирования состоит в воспроизведении поведения исследуемой системы на основе результатов анализа наиболее существенных взаимосвязей между ее элементами или другими словами — разработке симулятора (англ. simulation modeling) исследуемой предметной области для проведения различных экспериментов.
Рмитационное моделирование позволяет имитировать поведение системы РІРѕ времени. Причём плюсом является то, что временем РІ модели можно управлять: замедлять РІ случае СЃ быстропротекающими процессами Рё ускорять для моделирования систем СЃ медленной изменчивостью. Можно имитировать поведение тех объектов, реальные эксперименты СЃ которыми РґРѕСЂРѕРіРё, невозможны или опасны.
Рмитация, как метод решения нетривиальных задач, получила начальное развитие РІ СЃРІСЏР·Рё СЃ созданием РР’Рњ РІ 1950С… — 1960С… годах.
Можно выделить две разновидности имитации:
· Метод Монте-Карло (метод статистических испытаний);
· Метод имитационного моделирования (статистическое моделирование).
Области применения
· Бизнес процессы
· Боевые действия
· Динамика населения
· Дорожное движение
В· РРў-инфраструктура
· Математическое моделирование исторических процессов
· Пешеходная динамика
· Производство
· Рынок и конкуренция
· Сервисные центры
· Цепочки поставок
· Уличное движение
· Управление проектами
В· РРєРѕРЅРѕРјРёРєР° здравоохранения
В· Ркосистема
В· Рнформационная безопасность
Р‘РЛЕТ в„–6
Типы уроков информатики.
Р’ условиях внедрения РІ учебный процесс вычислительной техники учителю пришлось искать новые формы организации учебной деятельности для обеспечения наилучшего воспитательного Рё образовательного эффекта. Главным РїСЂРёР·Внаком СѓСЂРѕРєР° остается его дидактическая цель, показывающая Рє чему должен стремиться учитель. РџРѕ этому признаку можно выделить следуюВщие типы СѓСЂРѕРєРѕРІ информатики:
- урок сообщения новой информации (урок-объяснение);
- СѓСЂРѕРє закрепления Рё развития умений Рё навыков (тренировочВный) ;
- урок проверки знаний, умений и навыков.
Как правило, учитель ставит перед СЃРѕР±РѕР№ сразу несколько дидактиВческих целей, тогда структура СѓСЂРѕРєР° становится более сложной, такой СѓСЂРѕРє предусматривает смену различных РІРёРґРѕРІ деятельности Рё получает название комбинированного СѓСЂРѕРєР°.
Можно провести классификацию СѓСЂРѕРєР° информатики РїРѕ использованию Р’Рў. Рто:
- демонстрация - учитель показывает различ. эл-ты учебного материала: новые объекты языка, блок-схемы и т.д. Цель - сообщение нов. знаний. Дем-я отн-ся к типу "урок-объяснение";
- лабораторная работа (фронтальная) - одновременная работа учащихся РЅР° РџРР’Рњ СЃ программными СЃСЂ-вами или выполняет Рє.-Р». задание РЅР° изучаемом языке РїСЂРѕРіСЂ-СЏ. Роль учителя - наблюдение, оказание помощи. Лаб. раб. можно отнести Рє СѓСЂРѕРєСѓ закрепления РЅРѕРІ. мат-ла илик СѓСЂРѕРєСѓ проверки Р—РЈРќ;
- практикум - учащиеся получают индив. задания для протяжённой самост. работы. Работа уч-ся не регламентируется учителем.
Практика показала, что использование традиционных форм организаВции СѓСЂРѕРєРѕРІ информатики плохо способствует развитию коллективного творчества учащихся. Особенно хороша для коллективной работы так РЅР°Взываемая "творческая лаборатория". Такая форма работы позволяет учиВтелю решить сразу несколько проблем: недостаточное количество РєРѕРјВпьютеров РІ кабинете вычислительной техники Рё прививать учащимся РЅР°Ввыки коллективного труда. Работу "творческой лаборатории" учитель может организовать примерно следующим образом: класс делится учителем РЅР° РіСЂСѓРїРїС‹, состоящие РёР· 3-7 человек (РІ зависимости РѕС‚ сложности решаемой задачи), можно скомплектовать такие РіСЂСѓРїРїС‹ РїРѕ желанию учащихся, однако учителю следует проследить, чтобы качественный состав РіСЂСѓРїРїС‹ РЅРµ был однороден. Руководителя РіСЂСѓРїРїС‹ назначает сам учитель, причем этот ученик обязательно должен пользоваться авторитетом среди ребят ("лиВдер"). Перед началом работы учитель РїСЂРѕРІРѕРґРёС‚ беседу СЃ руководителями РіСЂСѓРїРї, разъясняет РёРј РёС… обязанности. Задание каждой РіСЂСѓРїРїРµ также выделяет учитель. Затем руководители РіСЂСѓРїРї распределяют это задание всем членам РіСЂСѓРїРїС‹ СЃ учетом РёС… способностей. Задание, как правило, рассчитано РЅР° 2 СѓСЂРѕРєР° Рё домашнюю работу. После выполнения заданий группами РїСЂРѕС…РѕРґРёС‚ РёС… защита. Для защиты задания РіСЂСѓРїРїР° выдвигает РѕРґВРЅРѕРіРѕ РёР· СЃРІРѕРёС… членов. После защиты учитель РІРЅРѕСЃРёС‚ СЃРІРѕРё замечания РїРѕ данной работе Рё аргументирует РёС…, Р° класс может согласиться СЃ этими замечаниями, Р° может Рё нет. Общее количество баллов Р·Р° работу РіСЂСѓРїВРїРµ выставляет класс (голосованием). Члены РіСЂСѓРїРїС‹ распределяют эти баллы между СЃРѕР±РѕР№ РїРѕ- степени участия каждого РІ выполненной работе.
Урок информатики должен состоять как минимум из двух основных частей. В первой части учителю необходимо ясно и доступно объяснить новый материал и проверить правильность усвоения учащимися его основных моментов.
Вторую часть СѓСЂРѕРєР° можно посвятить обсуждению РЅРѕРІРѕРіРѕ материала между учениками. РџСЂРё этом РѕРЅРё РјРѕРіСѓС‚ уже начать выполнять задания РЅР° РџРР’Рњ. Важно, чтобы школьники самостоятельно использовали "новые СЃРІРµВдения Рё имели возможность советоваться РґСЂСѓРі СЃ РґСЂСѓРіРѕРј. Если РІ первой части СѓСЂРѕРєР° учитель - лидер. РўРѕ РІРѕ второй части РѕРЅ - координатор, консультант РїРѕ сложным вопросам, РЅРѕ РЅРµ активный участник общения. Рксперимент показал, что РїСЂРё такой организации общения РЅР° СѓСЂРѕРєРµ РёРЅВформатики создаются благоприятные условия для усвоения материала.
.
3. Дана посл-ть действительных чисел а1,а2,…,аn. Заменить все её члены, большие данного Z, этим числом. Подсчитать количество замен.
program lab6;
type mas=array[1..100] of integer;
var a:mas;
i,j,z:integer;
begin
randomize;
for i:=1 to 10 do
begin
a[i]:=random(10);
write(a[i],' ');
end;
writeln('Vvedite Z');
readln(z);
j:=0;
for i:=1 to 10 do
begin
if a[i]>z then
begin
a[i]:=z;
j:=j+1;
end;
end;
for i:=1 to 10 do
write(a[i],' ');
writeln(j);
end.
Р‘РЛЕТ в„–7
Архитектура РР’Рњ
Рто, прежде всего, основные: устройства Рё блоки РР’Рњ, Р° также структура связей между РЅРёРјРё.
Общие принципы построения РР’Рњ, относящиеся Рє архитектуре:
-структура памяти РР’Рњ;
-способы доступа к памяти и внешним устройствам;
-возможность изменения конфигурации компьютера;
-система команд;
-форматы данных;
-организация интерфейса.
Архитектура - это наиболее общие принципы построения РР’Рњ, реализующие программное управление работой Рё взаимодействием основных ее функциональных узлов.
Классическая архитектура РР’Рњ Рё принципы Фон Неймана. РћСЃРЅРѕРІС‹ учения РѕР± архитектуре вычислительных машин заложил амер. математик Джон фон Нейман. РћРЅ РѕРґРёРЅ РёР· тех, кто убедительно обосновал использование двоичной системы для представления чисел (ранее РІСЃРµ Р’Рњ хранили обрабатываемые числа РІ десятичном РІРёРґРµ). Р’ дальнейшем РР’Рњ стали обрабатывать Рё РЅРµ числовые РІРёРґС‹ информации - текстовую, графическую, Р·РІСѓРєРѕРІСѓСЋ Рё РґСЂСѓРіРёРµ, РїРѕ двоичное кодирование данных РїРѕ - прежнему составляет информационную РѕСЃРЅРѕРІСѓ любого современного компьютера.
Рдея «хранимой программы»: первоначально программа задавалась путем установки перемычек РЅР° социальной коммутационной панели. Рто было весьма трудоемко. Поэтому Нейман РѕРґРёРЅ РёР· первых догадался, что программа может также храниться РІ РІРёРґРµ набора нулей Рё единиц, причем РІ той же памяти, что Рё обрабатываемые его числа.
Фон Нейман РЅРµ только выдвинул основополагающие принципы логического устройства РР’Рњ, РЅРѕ Рё предложил структуру, которая воспроизводилась РІ течение первых РґРІСѓС… поколений РР’Рњ.
Основными блоками по Нейману являются устройство управления (УУ) и арифметико - логическое устройство (АЛУ) (обычно объединяемые в центральный процессор), память, внешняя память, устройство ввода и вывода.
Следует отметить, что внешняя память отличается от устройств ввода и вывода тем, что данные в нее заносятся в виде, удобным компьютеру по недоступному для непосредственного восприятия человеком. Так, накопитель на магнитных дисках относится к внешней памяти, а клавиатура -устройство ввода, дисплей и печать - устройства вывода.
УУ и АЛУ в современных компьютерах объединены в один блок - процессор, являющийся преобразователем информации, поступающей из памяти и внешних устройств (сюда относятся выборка команд из памяти, кодирование и декодирование, выполнение различных, в том числе и арифметических операций, согласование работы узлов компьютера).
Архитектура РР’Рњ построенной РЅР° принципе Фон Неймана

Р’ построенной РїРѕ описанной схеме РР’Рњ РїСЂРѕРёСЃС…РѕРґРёС‚ последовательное считывание команд РёР· памяти Рё РёС… выполнение..
Разработанные фон Нейманом РѕСЃРЅРѕРІС‹ архитектуры вычислительных устройств получили РІ литературе название «фон-неймановской архитектуры». Подавляющее большинство вычислительных машин РЅР° сегодняшний день - фон-неймановские машины. Рсключение составляют лишь отдельные разновидности систем для параллельных вычислений, РІ которых отсутствует счетчик команд, РЅРµ реализована классическая концепция переменной Рё имеются РґСЂСѓРіРёРµ существенные принципиальные отличия РѕС‚ классической модели (примерами РјРѕРіСѓС‚ служить потоковая Рё редукционная вычислительные машины).
Р‘РЛЕТ в„–8
Ф-ии контроля знаний.
Проверочно-оценочная Дть Уля явл. неотъемлемой частью всей его пед работы и важным фактором улучшения качества обуч-я. Необходимо, чтобы контроль и оценка знаний отвечали общепед требов-м и вып-ли след.ф-ции:
1. учетная ф-я-системат-ая фиксация рез-ов обуч-я, что позвол.Улю судить об успеваемости каждого Ука, его достиж-ях и недочетов.
2. контрольно-корректир. ф-я- обеспечивает обратную связь «Уль-Ук»,необход для корректир-ки Улем своей методтки обуч-ия.
3. обуч-ая ф-я – проявл-ся в том, что в процессе проверки состояния ЗУН Уся происходит повторение матер-ла,Уль акцентрир. вним-е класса на главных вопросах, указ-ет на типичные ошибки, способствуя углублению знаний.
4. воспит-ая ф-ия –подразумевает стимулирование Уся к дальнейшей работе, углублению своих знаний. Оценивая состояние ЗУН,Уль не только констатирует состояние знаний, но и направляет его в учебн.работе, дает дополн.мотивацию в познават-ой Дти.
Недооценка учителями функций проверки и контроля знаний учащихся, как правило, приводит к снижению эффективности учебно-воспитательного процесса. Формы, средства и методы проверки должны быть разнообразными, в противном случае снижается возможность выявления результатов обучения.
3. Решите задачу линейного программирования симплексным методом. При решении задачи покажите умения отыскания исходного базиса с помощью введения искусственного базиса:
f=-5*x1+x2-x3→min,
3*x1+x2+x3 + x4 +x5=5,
2*x1 -x2 +3*x4 =4,
x1 +5*x2+6*x3+x4 =11.
G=u1+u2+u3→min,
U1+3*x1+x2+x3 + x4 +x5=5,
U2+2*x1 -x2 +3*x4 =4,
U3+x1 +5*x2+6*x3+x4 =11.
G=5-3x1-x2-x3-x4-x5+4-2x1+x2-3x4+11-x1-5x2-6x3-x4=20-6x1-5x2-7x3-5x4-x5=20-(6x1+5x2+7x3+5x4+x5);
| Базис пер | X1 | X2 | X3 | X4 | X5 | Своб чл |
| U1 | ||||||
| U2 | -1 | |||||
| U3 | ||||||
| G |
Min{5/3,4/2,11/1}={1.67,2,11}=1.67
| Базис пер | X1 | X2 | X3 | X4 | X5 | Своб чл |
| X1 | 0.33 | 0.33 | 0.33 | 0.33 | 1.67 | |
| U2 | -1.67 | -0.67 | 2.33 | -0.67 | 0.67 | |
| U3 | 4.67 | 5.67 | 0.67 | -0.33 | 9.33 | |
| G | -1 |
Min{1.67/0.33,9.33/4.67}={5.06,7.99}=1.99
| Базис пер | X1 | X2 | X3 | X4 | X5 | Своб чл |
| X1 | -0.07 | 0.29 | 0.36 | |||
| U2 | 1.36 | 2.57 | -0.79 | |||
| X3 | 1.21 | 0.14 | -0.07 | |||
| G | 1.36 | 2.57 | -0.79 |
Min{4/1.36,2/1.21}={2.94,1.65}=1.65
| Базиспер | X1 | X2 | X3 | X4 | X5 | Своб чл |
| X1 | 0.06 | 0.29 | 0.35 | 1.12 | ||
| U2 | -1.12 | 2.41 | -0.71 | 1.76 | ||
| X3 | 0.82 | 0.12 | -0.06 | 1.65 | ||
| G | -1.12 | 2.41 | -0.71 | 1.76 |
Min{1.12/0.29,1.76/2.41,1.65/0.12}={3.86,0.73,13.75}=0.73
| Базис пер | X1 | X2 | X3 | X4 | X5 | Своб чл |
| X1 | 0.2 | 0.44 | 0.9 | |||
| X4 | -0.46 | -0.29 | 0.73 | |||
| X3 | 0.88 | -0.02 | 1.56 | |||
| G |
X1=0.9-0.2x2-0.44x5
X3=1.56-0.88x2+0.02x5
X4=0.73+0.46x2+0.29x5
F=-5x1+x2-x3=5(0.9-0.2x2-0.44x5)+x2-1.56+0.88x2-0.02x5=4.5+x2+2.2x5+x2-1.56+0.88x2-0.02x5=-6.06+2.88x2+2.18x5=-6.06-(-2.88x2-2.18x5)
| Базис пер | X1 | X2 | X3 | X4 | X5 | Своб чл |
| X1 | 0.2 | 0.44 | 0.9 | |||
| X4 | -0.46 | -0.29 | 0.73 | |||
| X3 | 0.88 | -0.02 | 1.56 | |||
| F | -2.88 | -2.18 | -6.06 |
X*=(0.9,0,1.56,0.73,0)
Min f=-6.06
Р‘РЛЕТ в„–9
Основные понятия теории кодирования. Оптимальный код Шеннона-Фано.
Код — правило (алгоритме сопоставления каждом) конкретному сообщению строго
определенной комбинации символов (или сигналов). Кодом также называется отдельная комбинация таких символов. Для различия этих терминов, код в последнем значении еще называется кодовым словом.
Кодирование. Процесс преобразования сообщения в комбинацию символов в соответствии с кодом называется кодированием. Процесс восстановления сообщения из комбинации символов называется декодированием.
Операции кодирования и декодирования называются обратимыми, если их последовательное применение обеспечивает возврат к исходной информации без каких-либо потерь.
Алфавиты. Множество символов, при помощи которых записываются исходные сообщения называется первичным алфавитом, количество его элементов обозначается mI.
Множество символов, из которых могут состоять кодовые слова, называется
вторичным алфавитом, количество элементов этого множества обозначается m2.
Префиксное свойство. Префиксным называется код. не имеющий комбинации, которая была бы префиксом (начальной частью произвольной длины) любой другой комбинации того же кода.
Примером обратимого кодирования является представление знаков в телеграфном коде и их восстановление после передачи. Примером кодирования необратимого может служить перевод с одного естественного языка на другой - обратный перевод, вообще говоря, не восстанавливает исходного текста.
Шеннон ввел понятие избыточности - мера бесполезно совершаемых альтернативных выборов при чтении текста. Оптимальные способы кодирования уменьшают длину сообщения при передаче по каналу связи. Под термином «оптим. код» будем подразумевать коды с практически нулевой избыточностью. Кроме того, являясь оптим-м с т.зр. скорости передачи информации, код может быть не оптимальным с т.зр. предъявляемых к нему требований помехоустойчивости.
Главная идея кодирования Шеннона-Фано(ШФ)-заменить часто встречающиеся символы более короткими кодами, а редко встречающиеся- более длинными. Алгоритм основывается на кодах переменной длины. Для того, чтобы декомпрессор смог раскодировать сжатую последовательность, коды ШФ должны обладать уникальностью (каждый код уникально определяет один закодированный символ и не является префиксом любого другого кода).Рассмотрим алгоритм вычисления кодов ШФ. Например, последовательность aabbbccccddddd.Для вычисления кодов необходимо создать таблицу уникальных символов сообщения c(i) и их вероятностей p(c(i)), и отсортировать ее в порядке возрастания вероятности символов. C(i) p(c(i)) d 5/17, c 4/17, spase 3/17, b 3/17, a 2/17.
Далее таблица символов делится на две группы т.о., чтобы каждая из групп имела приблизительно одинаковую частоту по сумме символов. Первой группе устанавливается начало кода в «0», второй – в «1». Для вычисления следующих бит символов, данная процедура повторяется рекурсивно для каждой группы, в которой больше одного символа. Получаем: символ код d 00, c 01, spase 10, b 110, a 111.
Длина кода s(i) в полученной таблице равна int(-lg p(c(i))), если символы удалось разделить на группы с одинаковой частотой, в противном случае, длина кода равна int(-lg p(c(i)))+1. То есть int(-lg p(c(i)))<=s(i)<= int(-lg p(c(i)))+1.
Рспользуя полученную таблицу РєРѕРґРѕРІ, кодируем РІС…РѕРґРЅРѕР№ поток-заменяя каждый СЃРёРјРІРѕР» соответствующим РєРѕРґРѕРј. Естественно для рассжатия полученной последовательности, данную таблицу необходимо сохранять вместе сжатым потоком, что является РѕРґРЅРёРј РёР· недостатков данного метода. Р’ сжатом РІРёРґРµ таблица: 111111101101101101001010101100000000000 длиной 39 Р±РёС‚. Оригинал 139 Р±РёС‚. Коэффициент сжатия -28%.
Виды контроля знаний
Контроль направлен РЅР° получение информации, анализируя которую педагог РІРЅРѕСЃРёС‚ необходимые коррективы РІ течение учебно-воспитательного процесса. Рто может касаться изменения содержания, пересмотра РїРѕРґС…РѕРґР° Рє выбору форм Рё методов педагогической деятельности, или же принципиальной перестройки всей системы работы.
Следует различать значение отдельных видов контроля в учебном процессе:
-формирующего (текущего),
- зачетно-тематического,
- итогового.
РџРѕ результатам текущей проверки учитель решает, готовы ли школьники Рє усвоению последующего учебного материала. Отличительная особенность этого РІРёРґР° контроля заключается РІ том, что РѕРЅ проводится РЅР° всех этапах изучении темы или раздела. Поэтому РІ процессе текущего контроля РѕС‚ учащихся можно требовать знания только РЅР° том познавательном СѓСЂРѕРІРЅРµ, который предусмотрен определенным этапом овлаВдения учебным материалом. Завышение или занижение требований может привести Рє необоснованной оценке результатов обучения. Чтобы формирующий контроль стал эффективным, нужны разнообразные формы Рё средства РІ РёС… рациональном сочетании: фронтальные Рё индивидуальные, устные Рё письменные, рассчитанные РЅР° весь СѓСЂРѕРє или его часть. РљСЂРѕРјРµ того, учителю следует регулярно фиксировать результаты учебной деятельности учащихся. Чтобы подвести итоги обучения, учителю нужно знать Р·Р° усвоение какого материала Рё какие РІРёРґС‹ учебной деятельности ученику выставлена текущая оценка Такой учет может быть обеспечен тогда, РєРѕРіРґР° РІ классном журнале постоянно фиксируются темы СѓСЂРѕРєРѕРІ Рё содержание домашних заданий.
Для повышения объективности оценки нужно проводить итоговый контроль, С‚.Рµ. контроль РїРѕ итогам изучения темы или раздела учебного РєСѓСЂСЃР°. Рљ моменту завершения изучения темы, знания Сѓ учащихся, как правило, РІ РѕСЃРЅРѕРІРЅРѕРј сформированы Рё систематизированы. Цель такого контроля - выявление СѓСЂРѕРІРЅСЏ овладения основным содержанием темы, как каждым учащимся, так Рё классом РІ целом. Р’ содержание контроля должны войти основные РІРѕРїСЂРѕСЃС‹ темы, которые учитель отбирает РІ соответствии СЃ требованиями Рє результатам обучения. Ртоговая проверка планируется так, чтобы можно было проконтролировать усвоение школьВниками основных элементов программного материала. Если итоговая проверка показала, что учащиеся усвоили основные элементы программВРЅРѕРіРѕ материала, то РёС… знания РјРѕРіСѓС‚ быть оценены положительно.
Тематический контроль может проводиться РІ форме различного РІРёРґР° работ: письменная контрольная работа, зачетное занятие РїРѕ пройденВРЅРѕР№ теме. РџСЂРё проведении тематического контроля часть заданий должВРЅР° соответствовать деятельности РїРѕ образцу, часть - деятельности РІ измененной или РЅРѕРІРѕР№ ситуациях. Такая организация контроля РїСЂРµВдоставит каждому ученику возможность полностью проявить СЃРІРѕР№ СѓСЂРѕВвень подготовки РїРѕ теме.
Р‘РЛЕТ в„–10
Схема анализа урока
1. Общие сведения: дата, класс, школа, фамилия, имя, отчество учителя. Тема учебной программы, тема урока.
2. Соблюдение техники безопасности и санитарно-гигиенических норм работы с компьютером.
3. Структура СѓСЂРѕРєР°. Основные этапы СѓСЂРѕРєР°, назначение Рё длительность. Сочетание самоуправления Рё управления учителем. Рндивидуальная, парная, групповая Рё совместная работа класса. Ртапы повторения Рё закрепление материата. СЃРїРѕСЃРѕР±С‹
4. Цели, которые намечал учитель на урок, их достижение.
5. Сравнение содержания урока с материалом школьного учебника.
6. Оценка содержания урока с точки зрения обще дидактических принципов:
о научность - учет новейших достижений в информатике на уроке (понятие исполнителя, синтаксические диаграммы, доказательство правильности
алгоритмов и т.п.);
о наглядность — использование графической информации, таблиц исполнения алгоритмов, записи текстов с отступами и т.д.:
о последовательность — логическая стройность излагаемого материала. отсутствие пропусков в изложении, цикличность изучения сложных понятий;
о связь с практикой - прикладные задачи, ориентация содержания на требования жизни в компьютерном обществе.
7. Методы деятельности учителя на уроке. Привлечение учащихся для подготовки средств к уроку. Подготовка вычислительной техники в начале урока (или до него). Свобода учителя во владении материалом. Момент ответа на актуальные вопросы (по ходу урока или в конце). 11ндивид> ализация обучения — разные уровни заданий, привлечение сильных учащихся для помощи слабым и т.д. Приемы учителя для удержания внимания, действия при обнаружении ошибки на доске, в программе, в отчете.
8. Методы формирования Рё закрепления интереса Рє материалу. Стимулирование мыслительной деятельности учащихся. Рсточник заданий (РёР· учебника, РґСЂСѓРіРѕР№ литературы, изобретение учителем РїРѕ С…РѕРґСѓ СѓСЂРѕРєР°). Другие известные Рё нестандартные методы обучения, использованные РЅР° СѓСЂРѕРєРµ.
9. Работа Р·'чашихся РЅР° СѓСЂРѕРєРµ. Степень интереса Рє изучаемому материалу. Активность Рё самостоятельность обучаемых. Сознательность усвоения — усвоение смысла действий Р·Р° РР’Рњ. Доступность — стандартность терминологии, учет СѓСЂРѕРІРЅСЏ подготовленности класса, выделение уровней усвоения.
10. Рффективность обучения - насыщенность учебного времени, отсутствие постороннего материала, оптимальность выбора РџРЎ. Взаимоотношения учителя Рё учащихся: авторитарные, либеральные, сотрудничество. Организованность Рё дисциплинированность учащихся РЅР° СѓСЂРѕРєРµ - отношение Рє вычислительной технике, соблюдение техники безопасности РїСЂРё работе СЃ компьютером. Умение самостоятельно овладевать знаниями СЃ помощью справочного материала, компьютера, учебника.
11.
Последнее изменение этой страницы: 2016-08-11
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...