Условный экстремум: функция Лагранжа, метод множителей Лагранжа.

Конечномерной экстремальной задачей с ограничениями типа равенств называется задача в E_n:

Пусть XÍ E_n. Найти

F₀(x)®extr; (1)

при ограничениях: F_i(x)=0, i=1,…,m, x=(x₁, x₂, …, x_n), m<n, x Î X. (2)

Далее считаем, что все функции F_i (i=0, 1, … ,m) в X непрерывно дифференцируемы (в том смысле, что все частные производные ¶F_i / ¶x_i (k = 1, … , n) существуют и непрерывны в X).

В связи с этим вводится понятие условного экстремума.

Пусть Y множество точек x, для которых выполняется равенства (2). По определению точка x^*ÎX есть точка локального условного минимума (максимума) функции F₀(x) при наличии ограничений (2), если x^*ÎY и существует d > 0 такое, что для всех x ÎY, удовлетворяет неравенству:

имеет место

F₀(x)³ F₀(x^*), (в случае минимума)

F₀(x)£ F₀(x^*), (в случае максимума).

Точка локального условного максимума или минимума называется точкой локального экстремума.

По определению точка x^* Î X есть точка (глобального) условного минимума (максимума) функции F₀(x) при наличии ограничений (2), если x^*ÎY и имеет место для всех x Î X

F₀(x)³ F₀(x^*), (в случае минимума)

F₀(x)£ F₀(x^*), (в случае максимума).

Множество всех точек минимума и максимума функции на множестве Y принято называть точками экстремума функции на этом множестве или, просто, точками экстремума.

Отметим одну теорему из математического анализа:

Теорема Вейерштрасса.

Если функция u = f(x), xÎM (M Í Rⁿ), непрерывна на замкнутом ограниченном множестве M, то она достигает на этом множестве своих точных верхней и нижней граней (то есть решение задачи f(x) ® max (min) существует).

Следствие. Если функция u = f(x) непрерывна на Rⁿ и lim f(x) = + µ при x ® µ (lim f(x) = - µ при x ® µ), то f достигает своего абсолютного минимума (максимума) на любом замкнутом подмножестве R^*.

Это теорема и ее следствие часто используется при решении экстремальных задач и выступают самостоятельно и независимо от приведенных ниже методов.

Метод множителей Лагранжа является классическим методом решения экстремальных задач с ограничениями.

Классический подход к решению задачи (1), (2) дает метод множителей Лагранжа. Суть этого метода в следующем. Вводится функция Лагранжа

λ = (λ₀, λ_1, … _, λ_m) (3)

от переменных x₁, x₂, …, x_n, λ₀, λ_1, … _, λ_m, λ Î E_m+1.

Оказывается, если x^* = (x₁^*, x₂^*, …, x_n^*) – точка локального минимума или максимума функции F₀(x) на множестве X, то необходимо существуют числа (λ₀, λ_1, … _, λ_m), не равные все одновременно нулю, называемые множителями Лагранжа, также, что

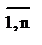, i = , (4)

то есть векторы

будут в точке x^* линейно зависимы.

Таким образом, для определения x^*, λ^* получается n+m уравнений:

с n+m+1 неизвестными. Следует учесть, что множителями Лагранжа определены при этом с точностью до пропорциональности. Если известно, что λ₀≠0, то можно, умножив все λ_i на константу, добиться равенства λ₀=1. Тогда число уравнений сравнятся с числом неизвестных. Однако заметим, что не исключен случай λ₀=0. Случай λ₀≠0 обосновывается следующим образом:

Для того чтобы λ₀≠0, достаточно, чтобы векторы F’₁(x^*), … , F’_m(x^*) были линейно независимы.

Действительно, векторы F’₀(x^*), F’₁(x^*), … , F’_m(x^*) образуют линейно зависимую систему. В нашем утверждении ее подсистема F’₁(x^*), … , F’_m(x^*) линейно независима, поэтому F’₀(x^*) можно линейно выразить через F’₁(x^*), … , F’_m(x^*), но тогда λ₀≠0.

Из этого следует правило решения задачи (1), (2).

Правило решения экстремальной задачи с ограничениями типа равенств.

1. Составить функцию Лагранжа

2. Выписать необходимое условие экстремума

(*)

3. Рассмотреть n уравнений (*) вместе с m уравнениями ограничениями

(**)

Полученная система содержит n+m уравнений с n+m+1 неизвестными x₁, x₂, …, x_n, λ₀, λ_1, … _, λ_m.

Несмотря на то, что система содержит число неизвестных на одно больше, чем число уравнений, данную систему можно свести к системе с n+m неизвестными, рассмотрев случаи λ₀=0 и λ₀≠0 (Чаще всего полагают λ₀=1 или λ₀=-1, когда λ₀≠0). Тогда в (*) – (**) число уравнений будет равно числу неизвестных.

4. Найти стационарные точки, то есть допустимые решения системы уравнений (*) – (**), в которой не все множители Лагранжа равны нулю.

Отыскать решение среди всех стационарных точек или доказать, что решения нет.