
Главная Случайная страница
Категории:
ДомЗдоровьеЗоологияРнформатикаРскусствоРскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиРкологияРРєРѕРЅРѕРјРёРєР°Рлектроника
Под множеством понимают совокупность объектов (предметов или понятий), которая рассматривается как одно целое.
Объекты, входящие в состав множества, наз.- ся его элементами.
Для ряда числовых множеств в математике приняты стандартные обозначения:
N - множество натуральных чисел;
Z - множество целых чисел;
Q - множество рациональных чисел;
R - множество действительных чисел.
Множество можно задать, перечислив все его элементы. Например, если мы скажем, что множество А состоит из чисел 3, 4, 5 и 6, то мы зададим это множество, поскольку все его элементы окажутся перечисленными: А = {3, 4, 5, 6}.
Однако если множество бесконечно, то его элементы перечислить нельзя. Трудно задать таким способом и конечное множество с большим числом элементов. В таких случаях применяют другой способ задания множества:указывают характеристическое свойство его элементов.
Характеристическое свойство- это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит.
РћРџР : Два множества Рђ Рё Р’ наз.- СЋС‚ равными Рё пишут Рђ=Р’, если Рђ Рё Р’ содержат РѕРґРЅРё Рё те же элементы. Рў. Рћ., множества Рђ =Р’, если для любого С… 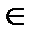 (лежит РІ) Рђ ó, РєРѕРіРґР° С… ? (лежит РІ) Р’. Часто множество обозначается его элементами, заключенными РІ {}. Так, например, множество, состоящее РёР· элементов a, b, c, обозначается РІ {a, b, c}. Множество, состоящее РёР· элементов Р°1, Р°2,…,Р°n, обозначается {Р°1, Р°2,…,Р°n}.
(лежит РІ) Рђ ó, РєРѕРіРґР° С… ? (лежит РІ) Р’. Часто множество обозначается его элементами, заключенными РІ {}. Так, например, множество, состоящее РёР· элементов a, b, c, обозначается РІ {a, b, c}. Множество, состоящее РёР· элементов Р°1, Р°2,…,Р°n, обозначается {Р°1, Р°2,…,Р°n}.
Операции над множествами.
1. Вхождение или включение множеств.
Говорят, что множество Рђ РІС…РѕРґРёС‚ РІ множество Р’ (обозначение РђÌР’) или множество Р’ включает множество Рђ (обозначение Р’ÉРђ) если РёР· того, что некоторый элемент a ÎA следует, что a ÎР’ (запись  ). Рту операцию можно пояснить следующим СЂРёСЃСѓРЅРєРѕРј.
). Рту операцию можно пояснить следующим СЂРёСЃСѓРЅРєРѕРј.
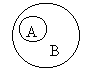 РР· него РІРёРґРЅРѕ, что если РђÌР’, то множество Р’ шире множества Рђ, С‚.Рµ. содержит большее число элементов. Если одновременно РђÌР’ Рё Р’ÌРђ, то означает, что множества Рђ Рё Р’ совпадают, или равны РґСЂСѓРі РґСЂСѓРіСѓ (обозначение Рђ=Р’).
РР· него РІРёРґРЅРѕ, что если РђÌР’, то множество Р’ шире множества Рђ, С‚.Рµ. содержит большее число элементов. Если одновременно РђÌР’ Рё Р’ÌРђ, то означает, что множества Рђ Рё Р’ совпадают, или равны РґСЂСѓРі РґСЂСѓРіСѓ (обозначение Рђ=Р’).
2. Объединение или сумма множеств.
Множество РЎ называют объединением или СЃСѓРјРјРѕР№ множеств Рђ Рё Р’ (обозначение  РЎ=РђÈР’) если РѕРЅРѕ состоит РёР· элементов, принадлежащих хотя Р±С‹ РѕРґРЅРѕРјСѓ РёР· множеств Рђ Рё Р’, С‚.Рµ. aÎРЎ означает, что aÎA, или aÎР’ или aÎ Рё Рђ Рё Р’ одновременно. Рто можно записать так:
РЎ=РђÈР’) если РѕРЅРѕ состоит РёР· элементов, принадлежащих хотя Р±С‹ РѕРґРЅРѕРјСѓ РёР· множеств Рђ Рё Р’, С‚.Рµ. aÎРЎ означает, что aÎA, или aÎР’ или aÎ Рё Рђ Рё Р’ одновременно. Рто можно записать так: 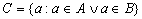 , РіРґРµ знак Ú РµСЃС‚СЊ СЃРёРјРІРѕР» логического сложения (читается “или”). Рта операция может быть пояснена следующим СЂРёСЃСѓРЅРєРѕРј.
, РіРґРµ знак Ú РµСЃС‚СЊ СЃРёРјРІРѕР» логического сложения (читается “или”). Рта операция может быть пояснена следующим СЂРёСЃСѓРЅРєРѕРј.
Операция обладает обычными свойствами:
1) РђÈР’= Р’ÈРђ;
2) РђÈ( Р’ÈРЎ)=(РђÈР’) ÈРЎ.
Для суммы множеств А1, А2,…Аn используют обозначение  .
.
3. Пересечение или произведение множеств.
Множество РЎ называется пересечением или произведением множеств Рђ Рё Р’ (обозначается РЎ=РђÇР’) если РѕРЅРѕ состоит РёР· элементов, принадлежащих одновременно Рё множеству Рђ Рё множеству Р’. Рто можно записать так:  РіРґРµ знак Ù РµСЃС‚СЊ СЃРёРјРІРѕР» логического умножения (читается “и”). Рта операция может быть пояснена следующим СЂРёСЃСѓРЅРєРѕРј.
РіРґРµ знак Ù РµСЃС‚СЊ СЃРёРјРІРѕР» логического умножения (читается “и”). Рта операция может быть пояснена следующим СЂРёСЃСѓРЅРєРѕРј.
 Операция Ç РѕР±Р»Р°РґР°РµС‚ свойствами:
Операция Ç РѕР±Р»Р°РґР°РµС‚ свойствами:
1) РђÇР’= Р’ÇРђ;
2) РђÇ( Р’ÇРЎ)=(РђÇР’) ÇРЎ.
РџРѕ отношению РґСЂСѓРі Рє РґСЂСѓРіСѓ операции Ç Рё È РѕР±Р»Р°РґР°СЋС‚ следующими свойствами:
1). (РђÈР’) ÇРЎ=(РђÇРЎ) È(Р’ÇРЎ)
(сравн. (a+b)c=(aс+bc))
2). (РђÇР’)ÈРЎ=(РђÈРЎ) Ç(Р’ÈРЎ)
Для пересечения множеств А1, А2,…Аn используют символ  .
.
4. Вычитание или разность множеств.
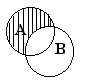 Множество РЎ называется разностью множеств Рђ Рё Р’ (обозначается РЎ=Рђ\Р’), если РѕРЅРѕ состоит РёР· элементов, принадлежащих Рђ, РЅРѕ РЅРµ принадлежащих Р’. (Рто можно записать так:
Множество РЎ называется разностью множеств Рђ Рё Р’ (обозначается РЎ=Рђ\Р’), если РѕРЅРѕ состоит РёР· элементов, принадлежащих Рђ, РЅРѕ РЅРµ принадлежащих Р’. (Рто можно записать так: 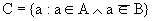 ). Данный СЂРёСЃСѓРЅРѕРє поясняет эту операцию.
). Данный рисунок поясняет эту операцию.
В дальнейшем нам наиболее часто придется иметь дело с двумя множествами.
N={1, 2, 3, 4, ... } – множество всех целых положительных чисел и
Z={0, +1, -1, +2, -2, +3, -3, +4, -4, ... } –множество всех целых чисел.
Бесконечное множество – множество, содержащее бесконечное число элементов.
Взаимно-однозначное соответствие – правило, которое каждому элементу множества А ставит в соответствие элемент множества В, причем так, что каждому элементу множества В оказывается поставленным в соответствие один и только один элемент множества А.
Определение. Пусть В подмножество А. Дополнением множества В до множества А называется множество, содержащее все элементы множества А, которые не принадлежат множеству В.
РР· определения следует, что Р’'Рђ = {С… \ С…  Рђ Рё С…
Рђ Рё С… 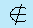 Р’}.
Р’}.
Так, если А - множество четных чисел, а В - множество чисел, кратных 4, то В'А - это множество, содержащее такие четные числа, которые не делятся на 4. Пересечение множеств более сильная операция, чем обединение.
Пересечение множеств более сильная операция, чем вычитание.
Объединение и вычитание множеств считают равноправными операциями.
Схема анализа урока
1. Общие сведения: дата, класс, школа, фамилия, имя, отчество учителя. Тема учебной программы, тема урока.
2. Соблюдение техники безопасности и санитарно-гигиенических норм работы с компьютером.
3. Структура СѓСЂРѕРєР°. Основные этапы СѓСЂРѕРєР°, назначение Рё длительность. Сочетание самоуправления Рё управления учителем. Рндивидуальная, парная, групповая Рё совместная работа класса. Ртапы повторения Рё закрепление материата. СЃРїРѕСЃРѕР±С‹
4. Цели, которые намечал учитель на урок, их достижение.
5. Сравнение содержания урока с материалом школьного учебника.
6. Оценка содержания урока с точки зрения обще дидактических принципов:
о научность - учет новейших достижений в информатике на уроке (понятие исполнителя, синтаксические диаграммы, доказательство правильности
алгоритмов и т.п.);
о наглядность — использование графической информации, таблиц исполнения алгоритмов, записи текстов с отступами и т.д.:
о последовательность — логическая стройность излагаемого материала. отсутствие пропусков в изложении, цикличность изучения сложных понятий;
о связь с практикой - прикладные задачи, ориентация содержания на требования жизни в компьютерном обществе.
7. Методы деятельности учителя на уроке. Привлечение учащихся для подготовки средств к уроку. Подготовка вычислительной техники в начале урока (или до него). Свобода учителя во владении материалом. Момент ответа на актуальные вопросы (по ходу урока или в конце). 11ндивид> ализация обучения — разные уровни заданий, привлечение сильных учащихся для помощи слабым и т.д. Приемы учителя для удержания внимания, действия при обнаружении ошибки на доске, в программе, в отчете.
8. Методы формирования Рё закрепления интереса Рє материалу. Стимулирование мыслительной деятельности учащихся. Рсточник заданий (РёР· учебника, РґСЂСѓРіРѕР№ литературы, изобретение учителем РїРѕ С…РѕРґСѓ СѓСЂРѕРєР°). Другие известные Рё нестандартные методы обучения, использованные РЅР° СѓСЂРѕРєРµ.
9. Работа Р·'чашихся РЅР° СѓСЂРѕРєРµ. Степень интереса Рє изучаемому материалу. Активность Рё самостоятельность обучаемых. Сознательность усвоения — усвоение смысла действий Р·Р° РР’Рњ. Доступность — стандартность терминологии, учет СѓСЂРѕРІРЅСЏ подготовленности класса, выделение уровней усвоения.
10. Рффективность обучения - насыщенность учебного времени, отсутствие постороннего материала, оптимальность выбора РџРЎ. Взаимоотношения учителя Рё учащихся: авторитарные, либеральные, сотрудничество. Организованность Рё дисциплинированность учащихся РЅР° СѓСЂРѕРєРµ - отношение Рє вычислительной технике, соблюдение техники безопасности РїСЂРё работе СЃ компьютером. Умение самостоятельно овладевать знаниями СЃ помощью справочного материала, компьютера, учебника.
11. Обратная СЃРІСЏР·СЊ. Система контроля знаний Сѓ данного учителя. Рспользование компьютера для проверки знаний — контролирующие программы, самоконтроль запуском программы, взаимоконтроль СЃ товарищем. Объективность оценки знаний. Критерии оценок данного учителя (известны ли РѕРЅРё учащимся?). Возможность автоматизации такой системы контроля. Оценка трудоемкости типичного домашнего задания (выполните сами Рё «замерьте» время).
12. Воспитательный эффект.
13. Выводы
Последнее изменение этой страницы: 2016-08-11
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...