
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Решите задачу линейного программирования графическим методом.
f=2x1+x2→min,
x1, x2  0,
0,
2x1+3x2  6,
6,
2x1+x2  4,
4,
x1  1,
1,
x1-x2 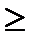 -1,
-1,
2x1+x2 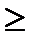 1.
1.
1) 2*x1 + 3*x2 = 6
| x1 | x2 |
2) 2*x1 + x2 = 4
| x1 | x2 |
3) x1 = 1
4) x1 – x2 = -1
| x1 | x2 |
| -1 |
5) 2*x1 + x2 = 1
| x1 | x2 |
| 0.5 |
Построим графики всех функций и найдем область, которую они ограничивают.
grad: (0,0) : (2,1).
Точка находится на пересечении 1 и 3 уравнений.
Решим систему:
2*x1 + x2 = 1
x2 = 0
x1 = 0.5
x2 = 0
f(max) = 2*0.5 + 0 = 1.
Проверим на Maple.
> with(plots);
> inequal({2*x1+3*x2<=6, 2*x1+x2<=4, x1<=1, x1-x2>=-1, 2*x1+x2>=1, x1>=0, x2>=0}, x1=-5..5, x2=-5..5, optionsfeasible=(color=blue),optionsexcluded=(color=white));

> with(simplex);
> minimize(2*x1+x2, {2*x1+3*x2<=6, 2*x1+x2<=4, x1<=1, x1-x2>=-1, 2*x1+x2>=1}, NONNEGATIVE);

БИЛЕТ №13
Метод производящих функций. Бином Ньютона  . Основные тождества с биномиальными коэффициентами.
. Основные тождества с биномиальными коэффициентами.
В комбинаторике производящая функция последовательности {  } — это формальный степенной ряд.
} — это формальный степенной ряд. 
Зачастую производящая функция последовательности чисел является рядом Тейлора некоторой аналитической функции, что может использоваться для изучения свойств самой последовательности. Однако, в общем случае производящая функция не обязана быть аналитической. Например, оба ряда
 и
и 
имеют радиус сходимости ноль, то есть расходятся во всех точках, кроме нуля, а в нуле оба равны 1, то есть как функции они совпадают; тем не менее, как формальные ряды они различаются.
Производящие функции дают возможность просто описывать многие сложные последовательности в комбинаторике, а иногда помогают найти для них явные формулы.
Метод производящих функций был разработан Эйлером в 1750-х годах.
Свойства
1.Производящая функция суммы (или разности) двух последовательностей равна сумме (или разности) соответствующих производящих функций.
2.Произведение производящих функций  и
и  последовательностей {an} и {bn} является производящей функцией свёртки
последовательностей {an} и {bn} является производящей функцией свёртки 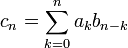 этих последовательностей:
этих последовательностей:
 .
.
Бино́м Нью́то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид
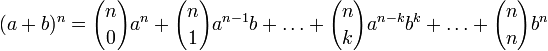
Где  — биномиальные коэффициенты, n — неотрицательное целое число.
— биномиальные коэффициенты, n — неотрицательное целое число.
Доказательство

Докажем это равенство индукцией по n:
База индукции: n = 1

Шаг индукции: Пусть утверждение для n верно:

Тогда надо доказать утверждение для n + 1:

Начнём доказательство:
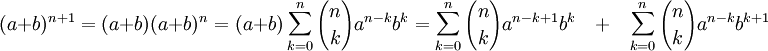
Извлечём из первой суммы слагаемое при k = 0

Теперь сложим преобразованные суммы:


Что и требовалось доказать.
В математике биномиальные коэффициенты — это коэффициенты в разложении бинома Ньютона 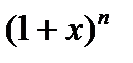 по степеням x. Коэффициент при
по степеням x. Коэффициент при  обозначается
обозначается  (иногда
(иногда  ) :
) :

Тождества
1. 
2. 
3. 
4. 
5. 
6. 
7. 

2. Дидактические требования к современному року
Реализация на уроке дидактических принципов. Вовлечение учащихся в постановку целей урока.
Постановка целей урока и определение системы задач, обеспечивающих ее достижение.
Формирование учебного материала с учетом потребностей и возможностей учащихся (коррекция, расширение, углубление).
Опора при изучении нового учебного материала на наличный опыт учащихся (знания, умения, навыки, привычки, отношения).
Соразмерность теоретической и практической насыщенности, направленности урока (теоретический и практических знаний, умений, навыков, задач)
Рационализация учебной деятельности, развитие и формирование общих учебных знаний, умений, навыков, привычек (компетентностей учебного назначения).
Использование стандартизированных форм представления учебного материала (структурно-логические схемы, опорные конспекты, фреймы), обеспечивающие сжатие учебной информации.
Реализация на основе принципа компенсации междисциплинарных учебных программ.
Выбор типа урока с учетом логики изучения учебной темы.
Выбор структуры урока адекватный типу урока.
Выбор средств и методов адекватных цели урока, его структуре.
Соразмерность репродуктивных (объяснительно-иллюстративный, репродуктивный), проблемного изложения и продуктивных (частично-поисковый, исследовательский) методов обучения.
Сочетание наглядно-образных, предметно-действенных и словестно-логических способов предъявления (усвоения) учебного материала.
Оптимальное сочетание фронтальных, групповых, парных, персонифицированных и коллективных форм организации учебной деятельности.
Повышение плотности урока (информативной, мыслительной, деятельностной).
Рациональное использование технических средств обучения, в том числе компьютеров.
Соразмерность учебного материала, изучаемого непосредственно на уроке и в форме домашнего задания.
Организация систематического повторения в различных формах (актуализация, входное, текущее, итоговое).
Организация на уроке обобщения и систематизации изученного учебного материала. Непрерывная активизации учебной деятельности учащихся. Систематическое использование межпредметных связей на уроке. Реализация воспитывающей функции обучения на уроке.
Оптимальное сочетания контроля, самоконтроля и взаимоконтроля для изучения уровня усвоения на уроке учебного материала.
Непрерывная ликвидация пробелов и недочетов в знаниях, умениях, навыках, привычках учащихся.
Управление ходом урока: распределение внимания; регулирование темпа учебной деятельности (говорение, чередование заданий, интенсивность дидактического взаимодействия и т.п.), осуществление обратной связи, коррекция хода урока (педагогическая импровизация).
Соблюдение единого орфографического режима
Последнее изменение этой страницы: 2016-08-11
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...