
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Задан некоторый набор товаров. Определить для каждого из товаров, какие из них имеются в каждом магазине и каких товаров нет ни в одном магазине.
program lab1;
const N=3;
type product = (bread, butter, cheese, milk);
assortiment = set of product;
stor = array[1..n] of assortiment;
var
m1:stor;
x:product;
a,b,c,xm1:assortiment;
i,j,iw,m:integer;
begin
for i:=1 to n do
begin
xm1:=[];
writeln('enter the number of product',i:2,'stor');
repeat
writeln('1: x:=bread; 2: x:=butter; 3: x:=cheese; 4: x:=milk; 5: break');
writeln('Vvedite 1 or 2 or 3 or 4 or 5');
read(iw);
case iw of
1: x:=bread;
2: x:=butter;
3: x:=cheese;
4: x:=milk;
5: break;
end;
xm1:=xm1+[x];
until iw=5;
m1[i]:=xm1;
end;
a:=m1[1];
c:=[bread..milk];
for i:=1 to n do
begin
b:=b+m1[i];
a:=a*m1[i];
c:=c-b;
end;
for i:=1 to 2 do
begin
case i of
1:writeln('products are in all stors:');
2:writeln('products arent in all stors:');
end;
for x:=bread to milk do
if x in a then
case x of
bread:writeln('bread');
butter:writeln('butter');
cheese:writeln('cheese');
milk:writeln('milk');
end;
if i=1 then a:=c;
end;
end.
БИЛЕТ №3
1. Алгебра высказываний как модель алгебры Буля, ее аксиоматическое задание. Принцип двойственности и теорема двойственности.
Высказыванием называется законченное повествовательное предложение, для кото-рого можно сказать истинно оно или ложно. Высказывание не м/б одновременно и истинным, и ложным.
Высказывания бывают атомарные (неделимые), или элементарные, исходные и сложные (составные).
Из элементарных высказываний с помощью операций над высказываниями или логических связок строят сложные высказывания.
Операции над высказываниями:
1. Операция конъюнкции ( /\ ).
Конъюнкцией двух высказываний, А и В, называется новое высказывание, обозначаемое (A /\ B), которое истинно тогда и только тогда, когда высказывания A и B истинны одновременно, и ложно во всех остальных случаях. Конъюнкции соответствует логическая связка "и".
2. Операция дизъюнкции ( \/ ).
Дизъюнкцией двух высказываний, А и В, называется новое высказывание, обозначаемое (A \/ B), которое истинно только тогда, когда истинно, по крайней мере, одно из высказываний, A или B, и ложно в единственном случае, когда оба высказывания, А и В, ложны. Дизъюнкции соответствует связка "или".
3. Операция следования или импликации ( → )
Импликацией (следованием) двух высказываний, А и В, называется новое высказывание, обозначаемое (A → B), которое ложно тогда и только тогда, когда A - истинно, а B - ложно, во всех остальных случаях высказывание (A→B) истинно. В высказывании (A → B) A - называется посылкой или антецедентом, B - следствием или консеквентом. Импликация (A → B) в разговорной речи имеет несколько разночтений: если A, то B;из A следует B;A влечет B;B следует из A;A достаточно для B;B необходимо для A.
4. Операция эквивалентности ( ↔ )
Эквивалентностью двух высказываний, A и B, называется новое высказывание, обозначаемое (A ↔ B), которое имеет значение ложь тогда и только тогда, когда A - истинно, а B - ложно или A - ложно, а B - истинно. А значение истина тогда и только тогда, когда одновременно оба высказывания, A и B, либо истинны, либо ложны. Эквивалентность (A ↔ B) в разговорной речи имеет несколько разночтений: A необходимо и достаточно для B; A тогда и только тогда, когда B; A эквивалентно B; A равносильно B; из A следует B , а из B следует A.
5. Операция отрицания() Отрицанием высказывания A называется новое высказывание, обозначаемое  , которое истинно тогда и только тогда, когда ложно A, и ложно тогда и только тогда, когда A истинно.
, которое истинно тогда и только тогда, когда ложно A, и ложно тогда и только тогда, когда A истинно.
Алгеброй Буляназывается непустое множество, содержащее, по крайней мере, два элемента и замкнутое относительно 2-ух бинарных операций: /\ и \/, удовлетворяющих законам: коммутативности (1), ассоциативности (2), дистрибутивности конъюнкции относительно дизъюнкции и дизъюнкции относительно конъюнкции (3), идемпотентности (4), сокращения (5), поглощения (6), противоречия для конъюнкции и исключения третьего для дизъюнкции (7), законам де Моргана (8) и закону двойного отрицания (9).
1. 


2. 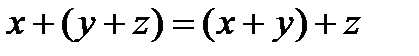
x * ( y * z ) = (x * y) * z
3. 
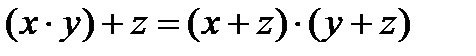
4. x * x = x
x + x =x
5. x * И = x
x + Л = x
6. x * Л = Л
x + И = И _
7. x * x = Л _
x + x = И
8. 
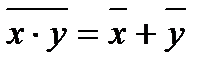
9. 
10. 
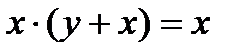
Последнее изменение этой страницы: 2016-08-11
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...