Основные комбинаторные объекты и числа.

Объекты:

а) система подмножеств множества E

E={e₁,e₂,…,e_n}, _n=({e₁},{e₂},…{e_n},{e₁,e₂}, ₃=({e₁},{e₂},{e₁e₂},{e₁e₃},{e₂e₃},{e₁e₂e₃},Ø)

Р±) сочетание элементов РёР· E РїРѕ k наз. упорядоченные подмножества РёР· k элементов, принадлежащих E.E={e₁e₂e₃}.

Сочетание РёР· E РїРѕ 2:{e₁,e₂},{e₁e₃},{e₂e₃}.

РІ) сочетание СЃ возможными повторениями РёР· E элементов РїРѕ k наз. неупоряд.Система РёР· k элементов, принадлеж. E. E={e₁e₂e₃}

Сочет. РёР· E РїРѕ 4: (e₁e₂ e₃ e₁), (e₁e₂ e₃ e₂)( e₁e₂ e₃ e₃)

Сочет. РёР· E РїРѕ 2: (e₁,e₂), (e₁e₃), (e₂e₃), (e₁e₁), (e₂e₂),(e₃e₃)

Рі) размещение элементов РёР· E РїРѕ k наз. упорядоченные РїРѕРґРјРЅРѕР¶-РІР° РёР· k элементов, принадл. E. E={e₁e₂e₃}

Размещ. РёР· E РїРѕ 2: (e₁e₂), (e₃e₁), (e₁e₃), (e₃e₁), (e₂e₃),(e₃e₂)

Рґ) перестановки элементов множества E наз. упорядочное множество РёР· всех n элементов РјРЅРѕР¶-РІР° E. E={e₁e₂e₃}

Перестановки РјРЅРѕР¶-РІР° E: (e₁e₂e₃), (e₁e₃e₂), (e₃e₁e₂),(e₃e₂e₁),(e₂e₁e₃),(e₂e₃e₁)

е) размещение с повторением элементов из E по k. Размещением с возможным повторением элементов из E по k наз. упорядоченные сист. Из k элементов, принадл.E, в кот. допускается повторение элементов.

Размещение РёР· E РїРѕ 2 СЃ возможн. повторениеми:(e₁e₂),(e₁e₃),(e₂e₃),(e₁e₁),(e₂e₂) (e₃e₃)

Р¶) разбиение множества E наз. неупорядочн. СЃРёСЃС‚. E₁,E₂,…E_K РёР· непустых подмножеств E Рё облад. следующими 2 свойствами:

1) Ek=E

2) E_i E_J =Ø, i J.

E={e₁e₂e₃}Разб. РјРЅРѕР¶-РІР°: ({e₁},{e₂e₃})

({e₁e₃},{e₂})

({e₁e₂},{e₃})

3) декартово произведение РјРЅРѕР¶-РІ A₁,A₂…A_N. A=A₁*A₂*…A_N.

A={x |x₁ 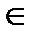A₁, x₂ 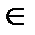A₂…,x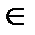_N A_N }

x= (x₁,x₂,x_N)

4) n-мерный куб разм. K =E_K*E_K…E_K

E_K={0, 1…k-1}

Числа:В основе подсчета числа комбинаторн. объектов лежат 2 простых правила:

1) Правило суммы: если свойством А обладает n предметов, а свойством В обладает m предметов, причем нет предметов, обладающ. свойствами А и В одновременно, то выбор предмета облад. либо свойством А, либо свойством В может быть осуществлен n+m способами.

2) Правило произведения: если элемент со свойством А может выть выбран n способами, а после выбора элемента со свойством А выбирается элемент со свойством В, кот. может быть выбран m способами, то пара (А,В) может быть выбрана nm способами.

а) число размещений из n элементов по k

E={e₁,e₂…e_N}

(a₁,a₂…a_K),a_i E

a₁-------n способами

a₂-------(n-1)СЃРїРѕСЃ.

a_K------(n-(k-1))

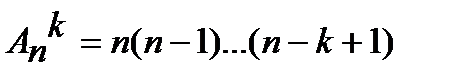
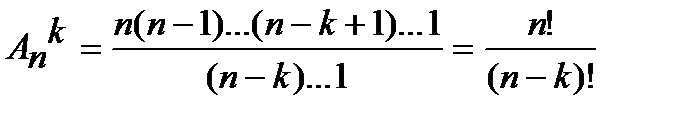
б) число размещений с возможн. повторением из n по k

E={e₁,e₂,…e_N}

(a₁,a₂,…a_K)

a₁--------n СЃРїРѕСЃРѕР±

a₂--------n СЃРїРѕСЃРѕР±

…

a_K--------n СЃРїРѕСЃРѕР±

в) число перестановок множества E, сост. из n элементов.

P_N,P_N=n!

(a₁,a₂,…a_N)

a₁--------n СЃРїРѕСЃРѕР±

a₂--------(n-1) СЃРїРѕСЃРѕР±

…

a_N-------1 СЃРїРѕСЃРѕР±

n(n-1)….1=n!

г) число сочетаний из n элементов по k без повторений.

E={e₁,…a_N}

(a₁,a₂…a_K)

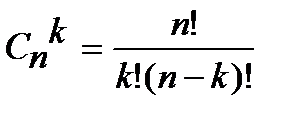
д) число сочетаний с возможными повторениями.

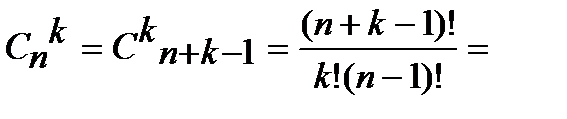
E={e₁,e₂,…e_N}

(a_q,a₂….a_K)

Типы уроков информатики.

В условиях внедрения в учебный процесс вычислительной техники учителю пришлось искать новые формы организации учебной деятельности для обеспечения наилучшего воспитательного и образовательного эффекта. Главным приз­наком урока остается его дидактическая цель, показывающая к чему должен стремиться учитель. По этому признаку можно выделить следую­щие типы уроков информатики:

- урок сообщения новой информации (урок-объяснение);

- урок закрепления и развития умений и навыков (тренировоч­ный) ;

- урок проверки знаний, умений и навыков.

Как правило, учитель ставит перед собой сразу несколько дидакти­ческих целей, тогда структура урока становится более сложной, такой урок предусматривает смену различных видов деятельности и получает название комбинированного урока.

Можно провести классификацию урока информатики по использованию ВТ. Это:

- демонстрация - учитель показывает различ. эл-ты учебного материала: новые объекты языка, блок-схемы и т.д. Цель - сообщение нов. знаний. Дем-я отн-ся к типу "урок-объяснение";

- лабораторная работа (фронтальная) - одновременная работа учащихся на ПЭВМ с программными ср-вами или выполняет к.-л. задание на изучаемом языке прогр-я. Роль учителя - наблюдение, оказание помощи. Лаб. раб. можно отнести к уроку закрепления нов. мат-ла илик уроку проверки ЗУН;

- практикум - учащиеся получают индив. задания для протяжённой самост. работы. Работа уч-ся не регламентируется учителем.

Практика показала, что использование традиционных форм организа­ции уроков информатики плохо способствует развитию коллективного творчества учащихся. Особенно хороша для коллективной работы так на­зываемая "творческая лаборатория". Такая форма работы позволяет учи­телю решить сразу несколько проблем: недостаточное количество ком­пьютеров в кабинете вычислительной техники и прививать учащимся на­выки коллективного труда. Работу "творческой лаборатории" учитель может организовать примерно следующим образом: класс делится учителем на группы, состоящие из 3-7 человек (в зависимости от сложности решаемой задачи), можно скомплектовать такие группы по желанию учащихся, однако учителю следует проследить, чтобы качественный состав группы не был однороден. Руководителя группы назначает сам учитель, причем этот ученик обязательно должен пользоваться авторитетом среди ребят ("ли­дер"). Перед началом работы учитель проводит беседу с руководителями групп, разъясняет им их обязанности. Задание каждой группе также выделяет учитель. Затем руководители групп распределяют это задание всем членам группы с учетом их способностей. Задание, как правило, рассчитано на 2 урока и домашнюю работу. После выполнения заданий группами проходит их защита. Для защиты задания группа выдвигает од­ного из своих членов. После защиты учитель вносит свои замечания по данной работе и аргументирует их, а класс может согласиться с этими замечаниями, а может и нет. Общее количество баллов за работу груп­пе выставляет класс (голосованием). Члены группы распределяют эти баллы между собой по- степени участия каждого в выполненной работе.

Урок информатики должен состоять как минимум из двух основных частей. В первой части учителю необходимо ясно и доступно объяснить новый материал и проверить правильность усвоения учащимися его основных моментов.

Вторую часть урока можно посвятить обсуждению нового материала между учениками. При этом они могут уже начать выполнять задания на ПЭВМ. Важно, чтобы школьники самостоятельно использовали "новые све­дения и имели возможность советоваться друг с другом. Если в первой части урока учитель - лидер. То во второй части он - координатор, консультант по сложным вопросам, но не активный участник общения. Эксперимент показал, что при такой организации общения на уроке ин­форматики создаются благоприятные условия для усвоения материала.

.

3. Дана посл-ть действительных чисел а1,а2,…,аn. Заменить все её члены, большие данного Z, этим числом. Подсчитать количество замен.

program lab6;

type mas=array[1..100] of integer;

var a:mas;

i,j,z:integer;

begin

randomize;

for i:=1 to 10 do

begin

a[i]:=random(10);

write(a[i],' ');

end;

writeln('Vvedite Z');

readln(z);

j:=0;

for i:=1 to 10 do

begin

if a[i]>z then

begin

a[i]:=z;

j:=j+1;

end;

end;

for i:=1 to 10 do

write(a[i],' ');

writeln(j);

end.

БИЛЕТ №7

Архитектура ЭВМ

Это, прежде всего, основные: устройства и блоки ЭВМ, а также структура связей между ними.

Общие принципы построения ЭВМ, относящиеся к архитектуре:

-структура памяти ЭВМ;

-способы доступа к памяти и внешним устройствам;

-возможность изменения конфигурации компьютера;

-система команд;

-форматы данных;

-организация интерфейса.

Архитектура - это наиболее общие принципы построения ЭВМ, реализующие программное управление работой и взаимодействием основных ее функциональных узлов.

Классическая архитектура ЭВМ и принципы Фон Неймана. Основы учения об архитектуре вычислительных машин заложил амер. математик Джон фон Нейман. Он один из тех, кто убедительно обосновал использование двоичной системы для представления чисел (ранее все ВМ хранили обрабатываемые числа в десятичном виде). В дальнейшем ЭВМ стали обрабатывать и не числовые виды информации - текстовую, графическую, звуковую и другие, по двоичное кодирование данных по - прежнему составляет информационную основу любого современного компьютера.

Идея «хранимой программы»: первоначально программа задавалась путем установки перемычек на социальной коммутационной панели. Это было весьма трудоемко. Поэтому Нейман один из первых догадался, что программа может также храниться в виде набора нулей и единиц, причем в той же памяти, что и обрабатываемые его числа.

Фон Нейман не только выдвинул основополагающие принципы логического устройства ЭВМ, но и предложил структуру, которая воспроизводилась в течение первых двух поколений ЭВМ.

Основными блоками по Нейману являются устройство управления (УУ) и арифметико - логическое устройство (АЛУ) (обычно объединяемые в центральный процессор), память, внешняя память, устройство ввода и вывода.

Следует отметить, что внешняя память отличается от устройств ввода и вывода тем, что данные в нее заносятся в виде, удобным компьютеру по недоступному для непосредственного восприятия человеком. Так, накопитель на магнитных дисках относится к внешней памяти, а клавиатура -устройство ввода, дисплей и печать - устройства вывода.

УУ и АЛУ в современных компьютерах объединены в один блок - процессор, являющийся преобразователем информации, поступающей из памяти и внешних устройств (сюда относятся выборка команд из памяти, кодирование и декодирование, выполнение различных, в том числе и арифметических операций, согласование работы узлов компьютера).

Архитектура ЭВМ построенной на принципе Фон Неймана

В построенной по описанной схеме ЭВМ происходит последовательное считывание команд из памяти и их выполнение..

Разработанные фон Нейманом основы архитектуры вычислительных устройств получили в литературе название «фон-неймановской архитектуры». Подавляющее большинство вычислительных машин на сегодняшний день - фон-неймановские машины. Исключение составляют лишь отдельные разновидности систем для параллельных вычислений, в которых отсутствует счетчик команд, не реализована классическая концепция переменной и имеются другие существенные принципиальные отличия от классической модели (примерами могут служить потоковая и редукционная вычислительные машины).