Метод простой итерации для СЛАУ

Метод Якоби — метод простой итерации для решения системы линейных алгебраических уравнений.

Постановка задачи

Возьмём систему линейных уравнений:

, РіРґРµ

Или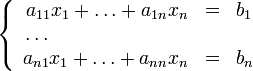

Описание метода

Для того, чтобы построить итеративную процедуру метода Якоби, необходимо провести предварительное преобразование системы уравнений к итерационному виду . Оно может быть осуществлено по одному из следующих правил:

где в принятых обозначениях D означает матрицу, у которой на главной диагонали стоят соответствующие элементы матрицы A, а все остальные нули; тогда как матрицы U и L содержат верхнюю и нижнюю треугольные части A, на главной диагонали которых нули, E — единичная матрица.

Тогда процедура нахождения решения имеет вид:

где k счётчик итерации.

В отличие от метода Гаусса-Зейделя мы не можем заменять на в процессе итерационной процедуры, т.к. эти значения понадобятся для остальных вычислений. Это наиболее значимое различие между методом Якоби и методом Гаусса-Зейделя решения СЛАУ. Таким образом на каждой итерации придётся хранить оба вектора приближений: старый и новый.

Условие сходимости

Приведем достаточное условие сходимости метода. Теорема.

Пусть . Тогда при любом выборе начального приближения :

1.метод сходится;

2.скорость сходимости метода равна скорости сходимости геометрической прогрессии со знаменателем ;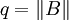

3.верна оценка погрешности: .

Условие остановки

Условие окончания итерационного процесса при достижении точности в упрощённой форме имеет вид:

(Существует более точное условие окончания итерационного процесса, которое более сложно и требует дополнительных

Понятие алгоритма.

Алгоритм –точный набор инструкций, описывающих порядок действий исполнителя для достижения результата решения задачи за конечное время. В старой трактовке вместо слова «порядок» использовалось слово «последовательность».

Базовые алгоритмические структуры

1. Следование и ветвление

2. Команды повторения

1) Цикл со счётчиком

2) Цикл с условием

3) Вложенный цикл

Базовая структура следование. Образуется из последовательности действий, следующих одно за другим.

Базовая структура ветвление. Обеспечивает в зависимости от результата проверки условия (да или нет) выбор одного из альтернативных путей работы алгоритма. Каждый из путей ведёт к общему выходу, так что работа алгоритма будет продолжаться независимо от того, какой путь будет выбран.

Ветвление используется в алгоритмах: когда надо пропустить какое-либо действие, выбрать одно из двух действий.

Структура ветвление существует в четырёх основных вариантов:

- если-то

- если-то-иначе

- выбор

- выбор-иначе

Команды повторения

Цикл со счётчиком

Обеспечивает многократное выполнение некоторой совокупности действий, которая называется телом цикла. Циклические алгоритмы бывают двух типов: циклы со счётчиком, в которых тело цикла выполняется определённое количество раз, циклы с условием, в которых тело цикла выполняется до тех пор, пока выполняется условие.

Когда заранее известно, какое количество раз необходимо выполнить телу цикла, то можно воспользоваться командой цикла со счётчиком.

нц для i от i1 до i2

тело цикла (последовательность действий)

РєС†

В начале выполнения цикла значение переменной счётчика устанавливается равным начальному значению. При каждом проходе цикла переменная счётчик увеличивается на величину шага. Если она достигает величины конечного значение, то цикл завершается и выполняются следующие за ним команды.

Цикл с условием

Часто бывает так, что необходимо повторять, тело цикла, но заранее не известно, какое количество раз это надо сделать. В таких случаях количество повторений зависит от некоторого условия. Условие выхода из цикла можно поставить перед циклом (цикл с предусловием) или после цикла (цикл с послеусловием).

Цикл типа пока

Предписывает выполнять тело цикла до тех пор, пока выполняется условие, записанное после слова пока. Как только условие стало принимать значение ложь, выполнение цикла заканчивается. Команды тела цикла могут не выполняться ни разу, если условие изначально не ложно.

Цикл с послеусловием сначала предписывает выполнение цикла, а затем проверку условия, и в этом случае команды тела цикла выполняются один раз обязательно.

Вложенные циклы

Возможны случаи, когда внутри тела цикла необходимо повторять некоторую последовательность операций, то есть организовать внутренний цикл. Такая структура получила название цикла в цикле или вложенный цикл. Глубина вложения циклов может быть различной. При использовании такой структуры для экономии машинного времени необходимо выносить из внутреннего цикла во вложенный все операторы, которые независимы от параметров внутреннего цикла.