Свойства алгоритмов. Формы представления алгоритмов.

Алгоритм –точный набор инструкций, описывающих порядок действий исполнителя для достижения результата решения задачи за конечное время. В старой трактовке вместо слова «порядок» использовалось слово «последовательность».

Свойства алгоритма:

Дана строка; слова разделены пробелами. Подсчитать, сколько в ней букв r, k, t.

program lab35;

var s:string;

n,i:integer;

begin

writeln('Vvedite stroku');

readln(s);

n:=0;

for i:=1 to length(s) do

if (s[i]='r') or (s[i]='k') or (s[i]='t') then

n:=n+1;

writeln('V stroke naydeni bukvi r, k, t : ', n, ' raz');

end.

БИЛЕТ №21

1.Метод трапеций для численного нахождения определенного интеграла: вывод формулы, оценка погрешности, геометрический смысл.

Метод трапеций.

При n=1 из формулы

(24) имеем (i=0;1):

РўРѕРіРґР° РїРѕ формуле (25) РЅР° отрезке [x₀;x₁] получаем интеграл:

(26)

Формула (26) даёт один из простейших способов вычисления определённого интеграла и называется формулой трапеций. Действительно, при n=1 подынтегральная функция заменяется интерполяционным многочленом Лагранжа первой степени (т.е. линейной функцией), а это означает геометрически, что площадь криволинейной фигуры подменяется площадью трапеции.

Распространяя формулу (26) на все отрезки разбиения, получим общую формулу трапеций для отрезка [a;b]

(27)

Если аналитическое выражение подынтегральной функции может быть поставлен вопрос об оценке погрешности численного интегрирования по формуле (27) (погрешность метода). В этом случае имеется в виду, что

РіРґРµ R_n(f) - остаточный член квадратурной формулы (27). Формулу остаточного члена получим вначале для отрезка [x₀;x₁]. Имеем:

откуда следует, что естественно рассматривать R как функцию шага h:R=R(h). Заметим, что R(0)=0.

Продифференцируем R(h) по h:

Заметим, что R'(0)=0. Далее:

(28)

Определим R, последовательно интегрируя R"(h) на отрезке [0;h]:

откуда с учётом (28) имеем:

(29)

Применяя к (29) обобщённую теорему о среднем, получаем:

(30)

РіРґРµ ζ_i?[x₀; x₀+h] Рё ζ_i зависит РѕС‚ h. Далее

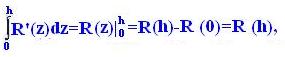
откуда с учётом (30) и обобщённой теоремы о среднем имеем:

(31)

РіРґРµ ζ?[x₀; x₀+h].

Таким образом, погрешность метода РїСЂРё интегрировании функции f РЅР° отрезке [x₀;x₁] РїРѕ формуле (27) имеет величину:

(32)

Из формулы (32) РІРёРґРЅРѕ, что РїСЂРё f’’(ζ)>0 формула (27) даёт значение интеграла СЃ избытком, Р° РїСЂРё f’’(ζ)<0 - СЃ недостатком.

При распространении оценки (32) на весь отрезок интегрирования [a;b] (т.е. на все n частичных отрезков) получается формула:

Учитывая, что h*n=b-a, найден следующий окончательный вид формулы для оценки погрешности метода интегрирования по формуле трапеций:

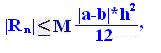РіРґРµ