Система методов преподавания информатики в школе. (Группы, методы)

Система методов преподавания информатики делится на группы:

1гр. По способу деятельности и степени самостоятельности:

-репродуктивный метод (неоднократное воспроизведение сообщенных сведений и способов деятельности для приобретения учащимися навыков и умений. Неоднократно исполняются команды для решения задач);

- частично-поисковый (для приближения учащихся к самостоятельному решению. Например, расчленение сложной задачи на серию доступных, приближающая к решению основной);

- исследовательский метод. (это «организация обучения, при котором учащиеся ставятся в положение исследователя: самостоятельно выделяют и ставят проблему, находят методы ее решения, исходя из известных данных, делают выводы и обобщения, постигают ведущие понятия и идеи, а не получают их в готовом виде».

Он формирует черты творческой деятельности, что является условием интереса);

2гр.По предъявлению материала:

-объяснительно-иллюстративный(Учитель дает готовый материал, а дети его воспроизводят и запоминают: осуществляется через устное слово, наглядные средства. Показ способов деятельности: слушают, читают, наблюдают, соотносят нов. Информацию с ранее усвоенной);

-наглядный;

-практический;

3гр.Модельный метод Аганесяна: исходное состояние - промежуточная деятельность-результат;

-проблемный метод (Учитель ставит проблему, сам ее решает, но при этом показ-т пути решения, раскрывает ходы решения);

-эвристический метод (частично-поисковый) (служит для постепенного приближения учащимися к самостоятельному решению проблем, но прежде следует научить выполнять отдельные шаги решения отдельных этапов исследования, формируя их умения постепенно. (Учитель ставит вопросы ученикам, делает выводы, высказывает предположение, строит план проверки))

3. Дана последовательность действительных чисел а1,а2,…,аn. Указать те элементы, которые принадлежат отрезку [c,d].

program lab42;

var

a:array [1..100] of integer;

i,k,c,d,n:integer;

begin

randomize;

writeln('Vvedite c and d:');

readln(c,d);

writeln('Vvedite kolvo elementov posledovatelnosti');

readln(n);

writeln('Elementi posledovatelnosti:');

for i:=1 to n do

begin

a[i]:=random(40);

write(a[i],' ');

end;

writeln;

write('Elementi posledovatelnosti iz [',c,',',d,']: ');

k:=0;

for i:=1 to n do

if (a[i]>=c) and (a[i]<=d) then

begin

write(a[i],' ');

k:=k+1;

end;

if k=0 then write('ne takih');

end.

БИЛЕТ №23

1. Симплекс-метод.

Рассмотрим задачу на минимум. Функция представлена в виде: 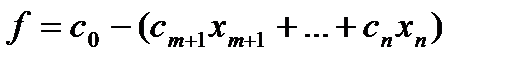(*). В зависимости от коэф-в здесь может быть два случая:

1) Все ≤0. Тогда значение функции уменьшить нельзя. Отсюда следует допустимое значение является оптимальным. .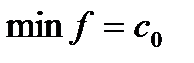

2) Среди чисел имеются полож-ные. Пусть , где m+1≤j≤n. Это позволит уменьшить значение функции путем увеличения j, оставив другие своб.члены нулевыми.

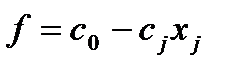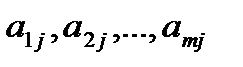(1) (2). Из (1)→увеличивая значения необходимо следить за сохранением условия неотрицательности базисных перем-х . Легко видеть, что при неотрицат-ти свободных членов , последние зависят от знака коэф-та перед . Два случая: 1) все числа , тогда значение может быть увеличено сколь угодно, что приведет к . 2) среди чисел имеются полож-е. 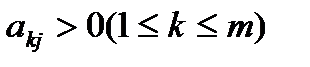. Предположим, что их несколько. Найдем для них значения: 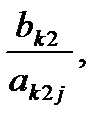… И выберем среди них наименьшее. Пусть 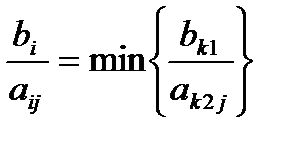. Обозначим его как 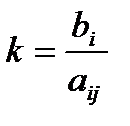. Тогда j увеличивается на не более, чем k. Коф-т 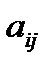наз-ся разрешающим элементом. Получим k= . Из (1) и (2) получаем значения: , ,…, ,…, . .

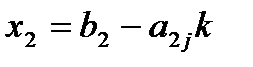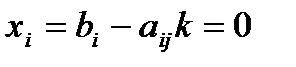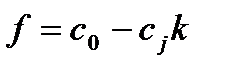Переменная должна перейти в состав свободных перем-х, а взамен него множество базисных переменных вводим в перем-е . Новый базис будет иметь вид: . Множество базисных переем-х будет таким 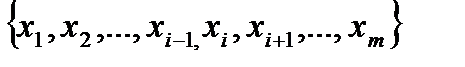. Значение функции 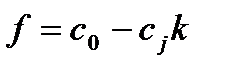≤0.

Для перехода к следующему шагу необходимо образовать систему ограничений в целевую функцию. С этой целью из уравнения системы, отвечающему бывшему базисному неизвестному 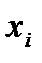выражаются новые базисные , которые вслед за этим исключаются из остальных уравнений системы. Исключается также из выражений для целевой функции. В результате получается новая система ограничений и новая целевая функция. Такие преобразования осуществляются методом Гаусса. Для таких преобразований обычно используются так называемые симплекс-таблицы, которые строятся из системы (3) и (*)

(3) имеет вид нарисовать таблицу

Затем по инструкции алгоритма получаем новую симплекс-таблицу. Если задача записана в виде (3) и (*) и все коэф-ты стоящие в скобке правой части (*) неположительные, то базисное решение 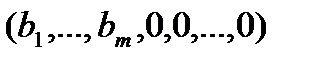является оптимальным и соответствует значению минимума, т.е. .

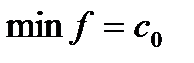Алгоритм для задачи на минимум.

1.Выяснить: имеются ли в последней строке таблицы положительные числа ( с₀ не принимается во внимание). Если все числа неположительны, то процесс закончен; базисное решение (b₁, b₂, ..., b_m, 0, 0,..., 0) является оптимальным; соответствующее значение целевой функции f = c₀. Если в последней строке имеются положительные числа, перейти к пункту 2.

2.Просмотреть столбец, соответствующий положительному числу из последней строки, и выяснить, имеются ли в нем положительные числа. Если ни в одном из таких столбцов j нет положительных чисел, то есть все числа a_1j, a_{2 j}, ..., a_{m j} неположительны для всех таких j, то значение х _j может быть увеличено неограниченно, что приведет к неограниченному уменьшению f, поэтому min ¦ = - ¥. Если найден столбец j, содержащий хотя бы один положительный элемент, то следует отметить этот столбец (такой столбец называется разрешающим) вертикальной стрелкой и перейти к пункту 3.

3.Разделить свободные члены на соответствующие положительные числа из разрешающего столбца и выбрать наименьшее частное. Отметить строку i таблицы, соответствующую наименьшему частному, горизонтальной стрелкой (такая строка называется разрешающей). Выделить разрешающий элемент a_ij, стоящий на пересечении строки i и столбца j. Перейти к пункту 4

4.Разделить элементы разрешающей строки исходной таблицы на разрешающий элемент. Полученная таким образом новая строка пишется на месте прежней в новой таблице. При этом в первом столбце для базисных переменных в новой таблице базисная переменная x_i заменяется на переменную x_j. Перейти к пункту 5.

5.Каждая следующая строка новой таблицы образуется сложением соответствующей строки исходной таблицы и строки записанной в пункте 4, которая предварительно умножается на такое число, чтобы в клетках выделенного столбца появились нули. На этом заполнение таблицы заканчивается, и происходит переход к пункту 1.